10.2.4.2. Houghton camera: plano-symmetrical corrector

For the fixed lens shape factor q, correction of aberrations is less flexible. Spherical can always be corrected, but zero coma requires particular corrector location (assuming stop at the corrector). The most interesting arrangement of this kind is a pair of plano-convex and plano-concave lenses with the lens shape factor q=1 for both elements (which means that the curved surface in both cases faces incoming light) of equal surface curvatures of the opposite sign. In this case, the lens element focal length (absolute value) cancelling spherical aberration of the mirror is, from Eq. 136, given by:

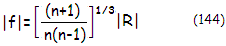
with R being, as before, the mirror radius of curvature. Needed radius of curvature (absolute value) for corrected spherical aberration for the two lenses is:

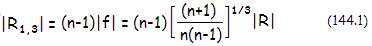
The lower-order coma coefficient of the corrector is constant, given by ccr=[(n+1)/n(n-1)]1/3/2R2, after substituting Eq. 144 into Eq. 138 and setting q=1. For zero coma, needed corrector location is, after setting Eq.140 to zero, given by:

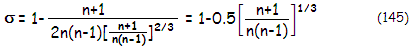
with σ being, as before, the mirror-to-corrector separation in units of the mirror r.o.c. For n=1.52, the zero coma corrector separation would be 0.264R (FIG. 193).

FIGURE 193: General prescription for plano-symmetrical Houghton corrector made of a pair of plano-concave and plano-convex lenses with equal curvatures of the opposite sign (plano-convex in front, curved sides of both lenses facing incoming light), can be made very simple for the Newtonian configuration. For given mirror radius of curvature R, needed surface radius of curvature (absolute value) for the two lenses is |R1,3|= (n-1)f1,3 = (n-1)[(n+1)/n(n-1)]1/3|R|. Lens thickness should be sufficient to resist flexure, and the two lenses are in contact or near-contact. Eq.145 gives needed separation for corrected coma. In general, it requires relatively large secondary, in proximity of D/2. In the Newtonian arrangement, with the corrector moved somewhat farther away from the mirror, in order to facilitate smaller obstruction by the diagonal flat, low residual coma remains, but it is insignificant for most practical purposes. Chromatic correction is not as good as with Schmidt corrector, but remains generally low with a single-glass corrector as long as mirror relative apertures do not exceed ~ƒ/2.5. It can be significantly reduced if corrector is made of two different glass types.

Note that these expressions use the thin lens approximation for primary aberrations, therefore they are not necessarily sufficiently accurate. While they are adequate for ~ƒ/4 and slower mirrors, raytracing and optimization are recommended when the primary mirror is of large relative aperture (~ƒ/3, and larger).

FIG. 194 illustrates Houghton camera performance at ƒ/3.

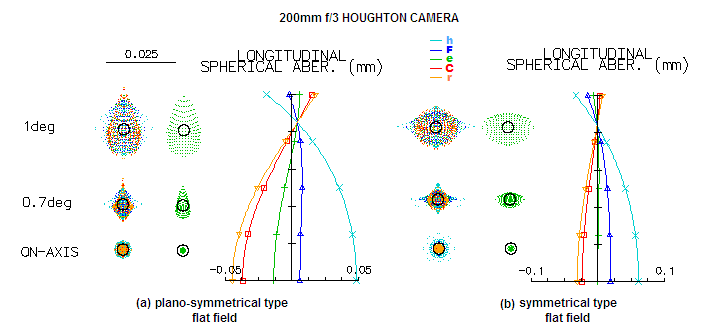
FIGURE 194: ƒ/3 Houghton camera with either plano-symmetrical (a) or symmetrical (b) corrector type still has very good color correction, with the limiting aberration being mirror astigmatism. Black circle represents e-line Airy disc. SPEC'S.

A few more words on interesting possibility of placing this type of the Houghton corrector between mirror and its focal plane, for cancelled spherical aberration and coma. Depending on the glass refractive index, the aplanatic corrector location is anywhere between ~0.7ƒ and ~0.5ƒ (ƒ=mirror focal length) from the mirror, for the glass index ~1.65 to ~1.5, respectively (Eq. 145). It offers good performance in an ultimately compact, easy to build camera-type instrument, with low astigmatism and, for most practical purposes, flat field (FIG. 195).

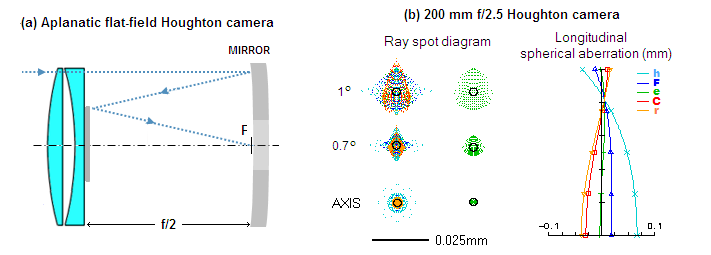
FIGURE 195: A super-compact Houghton camera with the corrector midway between the mirror and the image plane. The cone converging from the primary is reflected by a flat - or aluminized spot - at the rear corrector surface. With a common crown (n~1.52) needed minimum secondary size is nearly 0.5D; with a common flint (n~1.62), it is nearly 0.4D. Coma is corrected and the field is nearly flat. The only remaining aberration is astigmatism, but it is relatively low. Field quality and chromatism level are very similar to that of the Wright camera, but in a half as long instrument and with all-spherical surfaces. Main aberration in both, Houghton and Wright camera is astigmatism originating at the primary. In the Houghton, the primary astigmatism reduction due to the stop position is by a factor of (1-0.25)2, and in the Wright by a factor of (1-0.5)2. These reduction factors apply to the inherent mirror astigmatism, which is twice larger in the Wright camera, due to the mirror conic (K=1). In effect, Wright camera has 90% of the astigmatism of the Houghton. Obstruction size of the Houghton can be significantly reduced by using higher-index glass, and so can corrector's chromatism, by using slightly different glass types for the two elements. A BK8 substitution (for BK7) for the rear lens of the system shown, combined with the lens spacing increased to 14mm, results in the h-line RMS wavefront error reduced by nearly 50%, to 0.23 wave. SPEC'S

Another option of reducing the size of obstruction is inclusion of a simple sub-aperture corrector doublet to correct residual coma for stop positions farther away from the primary (FIG. 196). Aberration coefficients of the sub-aperture corrector are different than those given for the full-aperture, due to it being placed in a converging cone of light. Consequently, the position factor p for both lens elements of the sub-corrector has its value changed according to Eq. 97.

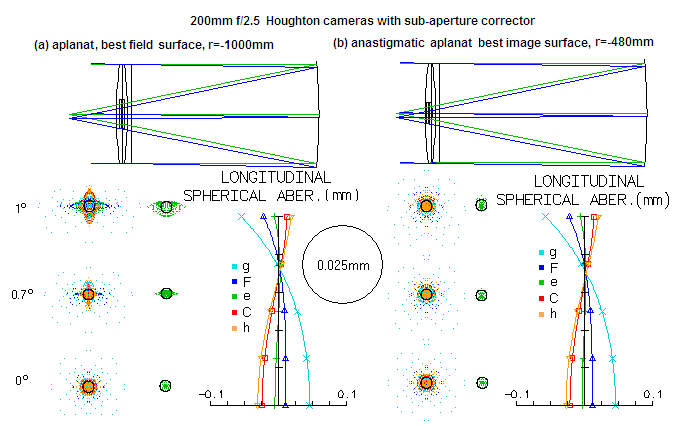
FIGURE 196: Two ƒ/2.5 Houghton-style cameras with accessible front focal surface and sub-aperture corrector placed within the full-aperture corrector (other configurations are possible). Off-axis correction is noticeably better than that of the flat-field aplanat. Configuration to the left (a) has all four lens radii of curvature identical, which allows merely cutting out the corrector elements from the full-aperture corrector. Design to the right (b) is corrected for both coma and astigmatism (slight trace of coma can be eliminated by optimizing). Field curvature in both arrangements is stronger, due to a lower, or no astigmatism. Chromatic correction is at a similar level in all three arrangements (black circle represents e-line Airy disc). SPEC'S

Use of the integrated sub-aperture corrector yields even better results in a two-mirror Houghton-Cassegrain camera. Due to compensating effect of the secondary's field curvature, it is possible to design a flat-field anastigmatic aplanat, with excellent color correction (FIG. 197).

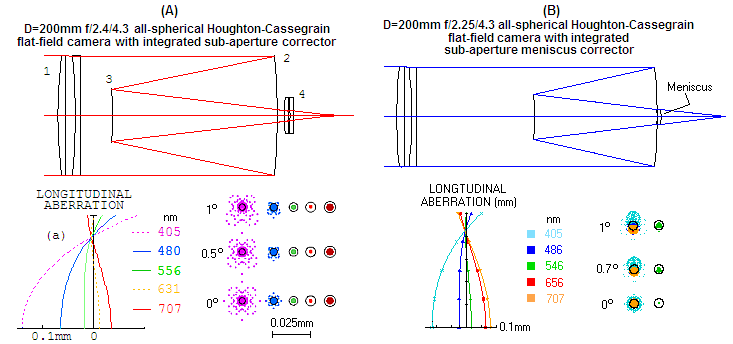
FIGURE 197: (A) Houghton-Cassegrain camera consisting of a full-aperture corrector (1), primary (2) and secondary (3) mirrors, and sub-aperture corrector (4) also consisting of a pair of plano-lenses; the system is a flat-field anastigmatic aplanat. The last three system elements (2,3,4) require spacing accuracy, but not out of the ordinary for this type of systems and the primary's relative aperture. The effect of achromatizing the full-aperture corrector (BCL22 replaced BK7) is mainly improvement in the violet end (roughly halved the h-line wavefront error), at a price of some error increase toward the red end (LA plots a and b for the "plain" and achromatized version, respectively). Better results are likely possible with more careful glass selection. Impeccable field quality extends without significant degradation beyond 2° off-axis (black circle represents e-line Airy disc). (B) Alternative configuration with meniscus corrector, less compact and with stronger astigmatism, but better chromatic balance. First four radii of curvature - two at the corrector, primary and secondary mirror - are identical. SPEC'S

This is not the best possible configuration, but it is illustrative of the level of correction achievable with this type of systems.

◄ 10.2.4.1. Houghton camera 1 ▐ 10.2.4.3. Houghton telescopes ►

Home | Comments