9.2 REFRACTING TELESCOPE OBJECTIVE: SEMI-APO AND APO

PAGE HIGHLIGHTS
• Apo definition • Polychromatic Strehl alternative • Glass matching and the relative partial dispersion diagram

Since the magnitude of secondary spectrum - which hereafter refers to the F/C vs. e-line focus separation, unless otherwise noted - depends on the specific dispersive properties of the glasses combined, some combinations will produce significantly more of it than common crown/flint combinations (for instance, as FIG. 148 illustrates, Schott N-KZFS2 and TIF3 would have it nearly 75% greater). On the other hand, some glass combinations will have it significantly smaller. The degree of reduction in secondary spectrum is determined by the ratio of their respective dispersion differentials between the blue (F) and red (C) line; if it is inversely proportional to the lens' powers, blue and red will be brought to a common (paraxial) focus (Eq. 44-45).

This implies that any two different glasses with their F-C dispersion differentials ratio sufficiently deviating from 1 can bring these two wavelengths to a common focus (obviously, two lenses made of the same glass will achieve this only for collimated beam). Since the formation of a real focus requires the positive element to be of greater optical power than the negative element, the former needs to have its C-F dispersion lower by the same ratio; in other words, the positive element of an achromat - or, for that matter, doublet objective - is always of weaker dispersion than the negative one.

But other wavelengths will still deviate from this common focus, creating secondary spectrum. The measure of its magnitude is, for the standard achromat with a common F/C focus, the axial separation between it and the e-line focus, which focuses the shortest. Its magnitude is directly proportional to how much the ratio between F-e dispersion differential between two glasses deviates from their F-C differential (Eq. 45.2). In the standard achromat, it is about f/1850, f being the objective's focal length.

If the ratio of the elements' respective dispersion differentials between the blue (F) and green (e) line is proportional to their F-C differential ratio, e line will be also brought to a common focus. This practically ensures that all other wavelengths will come to focus near to this common F-e-C focus as well. Such objectives qualify as apochromatic. Glass combinations that do not achieve this level of secondary spectrum correction, but are better corrected in that respect than standard achromats, are often referred to as semi-apo objectives.

But correcting for secondary spectrum alone does not guarantee chromatic performance significantly better - if at all - from an ordinary achromat's. The reason #1 is that the actual correction level in any refracting system varies significantly with the relative aperture. The reason #2 is that apochromatic objectives generally require significantly more strongly curved lens surfaces - in particular the two inner surfaces in a doublet objective - giving rise to potentially significant higher-order spherical aberration. More so considering that apochromatic objectives, due to their corrected secondary spectrum, are generally made in mid-to-fast focal ratios; while in fast achromats it is still secondary spectrum that dominates over spherochromatism (tertiary spectrum), in apochromats the latter becomes the dominant component of chromatic error.

That is why the so-called RC index, based on the size of the red (C) and blue (F) defocused blur cannot be used as a measure for chromatic correction in semi-apo, and particularly apo objectives. Whether calculated from a fraction of the focal length δ (RC=Dδ/2.44λF, where D is the lens diameter and 2.44λF the Airy disc diameter for optimized wavelength), or as a measured defocus Δ (RC=Δ/2.44λF²), it is relevant only for the defocus error with negligible spherochromatism. For instance, if a f/8 refractor has 0.1mm measured defocus for the best F/C focus (averaged), and no spherochromatism, its P-V wavefront error of defocus at the optimized wavelength's focus will be 0.1/8F², or 0.000195mm. If that best F/C focus has, say, 1/5 wave of primary spherical, at the optimized focus it will have about twice as much, or 0.4 waves (0.00022mm for 0.00055mm wavelength). And if at its best focus 0.1mm from the green focus it has 1/3 wave of spherical aberration, at the green focus it will be nearly 1/2 wave P-V of spherical aberration, and so on. Yet all three have identical RC ratio, based on the defocus distance alone. It is just as bad if a fraction of the focal length is used, because it is based on dispersion values that determine separation between paraxial foci, entirely neglecting possible spherochromatism.

The significance of Abbe (dispersion) differential between two glass elements is implied by Eq. 42: their respective Abbe numbers need to relate as the inverse of their focal lengths. Thus, the closer V1 and V2, the less of a relative differential between their focal length as well. And since the combined focal length is given by

(1/f) =(1/f1) +(1/f2),

the longer focal length always numerically negative, the smaller specific values for f1 and f2 need to be to generate a given combined focal length. And that means more strongly curved lens surfaces.

As long as higher-order spherical is negligible, spherical aberration can be practically cancelled in the optimized wavelength, with the residual increasing toward wavelengths farther away from it. It will keep increasing with the lens power for these "external" wavelengths, but will have no appreciable effect on the correction level in the optimized wavelength. However, since higher-order spherical aberration cannot be entirely removed, only minimized by balancing it with the lower-order form, it affects the optimized wavelength as well. To some extent, it is present in most apochromatic doublet objectives. After a certain point, spherochromatism can become intolerable; if pushed to far, it can be as crippling as secondary spectrum, particularly if the optimum wavelength (and, of course, those close to it) is significantly affected by higher-order spherical.

Due to the presence of spherochromatism, apochromats do not form common paraxial foci for F-e-C lines, rather common foci for given zonal heights, so called "crossings" (due to it, the paraxial foci are always separated, and could be more so in a fast apo than in a slow achromat). Ideally, non-optimized wavelengths should cross the optimized so that their best foci coincide; in practice, it is difficult to achieve. Since the magnitude of spherical aberration vary significantly (fourfold for the lower-order form) from its best focus to either paraxial or marginal focus, how close a crossing is - or not - to that ideal can cause significant difference in the chromatic correction level between two objectives formally satisfying the "three crossings" requirement.

In an attempt to define an apochromat as instrument meeting specific minimum correction level, it was stated by Ernst Abbe himself that an objective is apochromatic if its secondary spectrum is canceled and if its correction of spherochromatism - or tertiary spectrum - is also satisfactory.

Commonly cited definition giving specific numbers to the Abbe's principle above, which we'll call technical apo definition for a visual instrument, sets the specific limits to the wavefront error in the four non-optimized wavelengths spanning the visual spectrum to no more than 1/4 wave P-V in the F and C lines, and no more than 1/2 wave P-V in the g and r lines. If the wavefront error in the optimized wavelength is acceptably low (not specified), such objective is called a true apo. Obviously, both achromatic and apochromatic objectives could fulfill these conditions, with the former only requiring significantly smaller relative aperture. This creates ambiguity, which is not remedied by the use of a term apochromatic performance, as implying negligible chromatic error. For instance, lens objective passing the 1/4 wave F/C requirement, with as little as 1/15 wave P-V error in the optimized wavelength still can have only 0.93 polychromatic Strehl. With a more down-to-earth optimized line correction of 1/8 wave P-V, which by pretty much anyone's definition of "corrected" fits in, the Strehl is down to 0.9.

Put simply, the term apochromatic specifically implies the mode of chromatic correction, not the level of optical quality. For that, we have and should use appropriate parameters from the realm of optical aberrations.

It should be noted that this technical apo definition itself is not well defined, since it does not specify which form of spherical aberration its P-V wavefront error criteria refer to (it could be even referring to defocus error, which would only make it more useless). Presumably, it is for primary spherical, the balanced (mid focus) form, but the problem is that apo objectives can and do generate all forms of spherical aberration: primary, pure secondary, balanced secondary, and all degrees of mixture between primary and secondary spherical and defocus. With the form of the aberration, its P-V/RMS ratio also changes, from √11.25 with the primary, to √28 with balanced secondary spherical. Since it is the RMS wavefront error that determines transfer of energy toward outer areas of point image, secondary spherical has comparable effect to that of balanced primary spherical when the P-V wavefront error of the former is greater by a factor √28/11.25, or nearly 1.6. For clarity's sake, such definition should use the RMS wavefront error.

Another inadequacy of the technical definition of a "true apo" comes from the fact that refracting objective does not necessarily need to achieve the theoretical requirement for an apo - three widely separated wavelengths with a common focus - in order to have its chromatic error reduced to negligible. Based on the technical definition, a 100mm f/12 refracting objective needs to have secondary spectrum reduced between 4 and 10 times vs. standard achromat (1 wave P-V of defocus in the C and F, 1.8 in the red r, and 4.9 waves in the violet g), in order to reach the "true apo" level. An f>/6 objective, twice as much. There is no clear-cut line, since reducing the secondary spectrum by a factor of 0.25, or little more, at f/12 (i.e. going to f/48), will bring three of the four wavelengths below the true apo minimum, but the fourth one, g, would still be well over twice the allowed maximum. Yet, the photopic Strehl exceeds 0.96, which is at least as good indicator of high correction level as any technical definition.

On the other hand, reducing relative aperture as required to bring g-line below the maximum allowed by the technical apo definition, which for 100mm objective requires f/120, would result in the other three becoming negligibly small, with the overall chromatic correction - approaching 0.99 polychromatic photopic Strehl - significantly better than the minimum true apo requirement (low residual secondary spectrum matters little anyway, since even the true apos have their paraxial g, F, e, C and r foci separated due to spherochromatism).

In fact, reaching the minimum of sensibly perfect chromatic visual correction does not necessarily require apochromatic condition, i.e. the absence of secondary spectrum. Common achromat becomes sensibly perfect with respect to its chromatic correction if of sufficiently small relative aperture. A 100mm aperture standard achromat just exceeds 0.95 visual polychromatic Strehl at f/36, which implies that a threefold reduction in secondary spectrum - or down from 0.00054f to about 0.00018f - would do it for an f/12 objective, assuming that spherochromatism remains negligible (this is the case, in general, with objectives ~f/12 and slower). That despite having 1/3 wave P-V defocus error in the F and C lines averaged, nearly 0.6 wave in r and over 1.5 wave in the g. The near perfect correction in the extended sub-range around optimized wavelength compensates for that. Similarly, an f/6 objective would require sixfold reduction in the secondary spectrum of the standard achromat. Such sensibly perfect semi-apo (technically) would likely be noticeably more "colorful" than an apo of a similar polychromatic Strehl - primarily in showing faint violet halo around bright objects - but that, according to raytrace, wouldn't make it inferior contrast-wise. It would have slightly lower contrast transfer for large details, but slightly better near the limit of resolution.

In the context of detector sensitivity, the technical apo definition fails to specify which sensitivity mode it applies to. Presumably, it should be for the night observing eye sensitivity mode, generally mesopic, but if so, the limits are determined entirely arbitrarily. There is no criteria for other detector sensitivity modes, including CCD.

Ambiguity of using term apochromatic to define some minimum level of chromatic correction is compounded by the use, in the same manner, of undefined term semi-apo, which in general should imply significantly smaller secondary spectrum than in an achromat, but still appreciable in comparison to an apo. So, depending on the definition of "significant" and "appreciable", a semi-apo can span the range from little better than an achromat to nearly as good as an apo. Since, as pointed out, neither has a determined level of optical correction, each being just a mode of chromatic correction, same applies to the semi-apo: it should only be used to implicate mode of chromatic correction - refracting objective with less secondary spectrum than standard achromat, but not fulfilling the condition of bringing three widely spaced wavelengths to a common focus.

Summing it up, again, none of the terms, achromatic, apochromatic, nor semi-apo, is well suited to describe the level of optical quality of refracting objective. Their original meaning is to indicate specific mode of chromatic correction, and should only be used in that context.

Alternately, modern ray tracing programs allow us to specify the level of optical quality of the refracting objective with a single number: polychromatic Strehl (SP), expressing the relative peak diffraction intensity vs. aberration-free aperture. Also, it directly implies the relative contrast loss averaged over the range of MTF frequencies as (1-SP). In this context, we could define apochromatic objective as one having polychromatic Strehl 0.95 or higher, but it would still induce ambiguity, and isn't really necessary. Optical quality of a refracting objective can be simply ranked according to its polychromatic Strehl as:

CORRECTION LEVEL	POLYCHROMATIC STREHL	COMPARABLE LEVEL OF BALANCED PRIMARY SPHERICAL ABERRATION
"sensibly perfect"	SP>0.95	better than 1/8 wave P-V
"excellent"	0.95>SP>0.9	1/8 to 1/6 wave P-V
"good"	0.9>SP>0.8	1/6 to 1/4 wave P-V
"fair"	0.8>SP>0.7	1/4 to 1/3.2 wave P-V
"poor"	0.7>SP>0.6	1/3.2 to 1/2.6 wave P-V
"bad"	0.6>SP>0.4	1/2.6 to 1/2 wave P-V
"useless"	SP<0.4	worse than 1/2 wave P-V

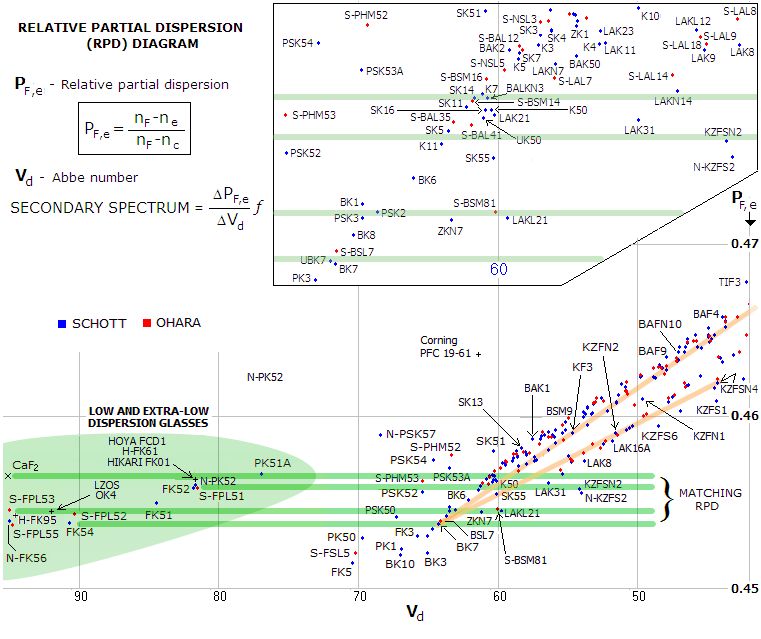
making the effect of any form of chromatism comparable to monochromatic aberrations (note that this classification applies to the common amateur aperture range for refractors, of less than about 8 inch in diameter; in significantly larger refractors the extra aperture can in part compensate for the higher chromatic error).

Polychromatic Strehl can be based on either visual sensitivity, or that of a detector. In general, the former would be sensitive to the correction level in the narrow range of high-sensitivity wavelengths, while tolerant of larger errors over the wavelengths of lower eye sensitivity. The latter, on the other hand, would require better correction toward the ends of visual spectrum, and beyond (average CCD sensitivity is about 70% at the ends of visual spectrum), although that correction level could be - and usually has to be - somewhat lower than that for the high-sensitivity wavelengths in the visual mode.

The advantages of using polychromatic Strehl for defining the level of chromatic correction are obvious. Now we can put it, say, as 0.9 visual Strehl apo, 0.84 visual Strehl semi-apo, or 0.77 visual Strehl achromat, describing both, actual correction level and the mode of correction (i.e. objective type) in as few words as possible. No more guessing: is the apo "true" or not, how far ahead it is of the achromat, how good is the semi-apo, etc.

In the case of apo objective, polychromatic Strehl also expresses the effect of correction level near the optimized wavelength, not specified in the technical definition. This correction level has significant consequences for the overall correction level, approximately lowering the Strehl by the degradation factor equal to its Strehl corresponding to the error level for spherical aberration. For instance, the conventional "diffraction limited" correction level 0f 0.074 wave RMS wavefront error in the optimized wavelength will reduce the polychromatic Strehl approximately by a factor of 0.8 - from, say, 0.95 with negligible optimized-line error, to 0.76. Even a 0.05 wave RMS (comparable to 1/6 wave P-V of lower-order spherical aberration) in the optimized wavelength will lower the Strehl by about 5% vs. 0.037 wave RMS correction level (comparable to 1/8 wave P-V). The effect of correction error in the optimized wavelength on the overall chromatic correction is shown on FIG. 176 for an SCT.

Going back to the correction mode for chromatism in the refracting objective, whether it is achromatic, with a common paraxial focus for two widely separated wavelengths, or apochromatic, with a third, mid-range wavelength also brought to the common focus, is determined by the dispersive properties of glasses combined. Specifically, secondary spectrum, defined as the separation between common F/C and green e-line focus, is proportional to the ratio of relative partial dispersion (PF,e) differential vs. Abbe number (Vd) differential for the two glasses in combination (FIG. 148). Graphically, two glasses will have near-zero secondary spectrum if the line connecting them on a relative partial dispersion diagram is near horizontal, i.e. if their respective relative partial dispersion values are nearly identical.

FIGURE 148: Cancelling out secondary spectrum requires two glass elements with nearly identical relative partial dispersion (RPD) value. Since one of them is of positive, and the other of negative power, their refractive variation with the wavelength offsets one another, with the dispersion (Abbe number) differential compensating for the difference in power (the weaker, negative element, has to have higher dispersion). On the RPD graph, near zero RPD differential translates into near horizontal line connecting two glasses. Thus, the greater slope of the connecting line, the more of secondary spectrum produced; for instance, top orange line connects BK7 crown and F2 flint, the standard achromat, while the lower orange line, connecting BK7 and KZFSN4 indicates nearly 30% smaller secondary spectrum (#2 in Table 12). For given RPD differential, secondary spectrum is inversely proportional to the Abbe number differential between two glasses.
The Abbe differential is also important because it determines lens power needed for achieving the minimum secondary spectrum level for the two glasses: the smaller differential, the stronger lenses required. That, however, ultimately generates unacceptable level of spherochromatism, both from primary spherical (which only affects non-optimized wavelengths), and also from secondary spherical, which is generally smaller in magnitude. The former only affects non-optimized wavelengths, but the latter affects optimized wavelength as well, since secondary spherical in the objective with spherical surfaces can be only minimized to 1/5 to 1/6 of its magnitude, by balancing it with primary spherical of opposite sign. Fast doublets (~f/8 and faster) require Abbe differential of ~25, or greater; this is why very-low-dispersion glasses (at left, shaded green) are necessary for such systems (important factor here is also the refractive index match; the stronger index in the matching glass, the weaker its required power, and vice versa, which favorably or unfavorably alters the secondary spherical differential - i.e. secondary spherical residual - on the strongly curved surfaces, particularly those of fast doublets).
In a triplet, the extra element reduces the individual surface curvatures, making it possible to use glasses with significantly smaller Abbe differential than doublet, as well as making faster objectives for a given Abbe differential. It is simply that instead of a single pair of inner radii between two glasses, now we have two pairs, hence they need to be only about half as strong to produce the same power. This greatly reduces the higher-order spherical aberration residual, which limits how fast a refractive objective can go - in addition to spherochromatism, which is also f-ratio dependant. Adding the third lens element does not affect secondary spectrum, as long as this third element is of the same type as one of the two other glasses. Adding different third glass introduces secondary spectrum proportional to the RPD differential between it and the element of opposite power, modified by the respective powers of the elements. This allows correcting for secondary spectrum in a triplet with the two elements of identical power sign having near identical non-zero RPD differential vs. central element of opposite sign, thus with their individual secondary spectrum contributions nearly canceling out.

As FIG. 148 shows, some dozen, or so, extra low-dispersion glasses can be matched by roughly twice as many higher dispersion ("normal" or slightly "abnormal") glasses for cancelling secondary spectrum. However, while they'll bring blue, green and red to a common focus, their dispersion properties toward violet and deep red vary (according to their RPD for those wavelengths), making some combinations better than others with respect to the degree of correction in that spectral range. Since it is usually the error toward violet that dominates, it can be helpful to include in consideration the g-line secondary spectrum (i.e. separation between g-line and common F/C focus) which is indicated on the Pg,F RPD diagram below.

It is also only the lower portion of the complete diagram, with glasses relatively close in RPD to the extra low dispersion glasses (diagram shows mostly Schott glasses, but nearly all non-ED glasses from other suppliers also fall around the same upward diagonal, most of them near-equivalent or close to the Schott glasses). It is generally similar to the PF,e RPD diagram, but not identical. Green shaded area outlines, approximately, glasses which are a good match to the ED glasses at left, i.e. those with small Pg,F differential, with which they would have violet g-line focus close to the common F/C focus. Obviously, if the two glasses also have a small PF,e differential, all three - C, F, g and e paraxial focus will be close together (how close is also influenced by the Vd differential, but that factor becomes unimportant as the RPD differential becomes negligibly small).

The limitation to the diagram accuracy in predicting the magnitude of chromatism is still the same, since it reflects location of paraxial foci of other wavelengths when F and C focus nearly coincide, hence does not account for spherochromatism. With significant spherical aberration in non-optimized wavelengths, their respective best foci shift away from their paraxial foci, and chromatism becomes significant regardless of the glass combination formally having negligible secondary spectrum. For g-line specifically, it is, in general, beneficial to have RPD differential not significantly larger than in PF,e, because it generally has more of spherical aberration than shorter wavelengths, shifting its best focus farther away from its paraxial focus. When it is larger, the violet - and particularly its best focus - is pushed farther out, away from the rest of wavelengths.

It is illustrated with plots below the diagram. Leftmost, the glass combination has very small RPD differential, not only PF,e (e-line vs. common F/C focus), but also Pg,F, with the paraxial g-line focus very close to the common paraxial F/C focus. Magnified focal zone above shows that the g-line paraxial focus is only a small fraction of a mm from the common F/C focus (paraxial r-line focus, reflecting the PC,r RPD value, is also very close). However, due to the presence of spherochromatism, each wavelength has longitudinal aberration, i.e. the focus location varies with zonal height in the pupil, with the best focus location being approximately that for 0.7 zone (since only a small amount of secondary spherical is present, bending all non-optimized wavelengths slightly to the right toward top, best focus location in slightly above 0.7 zone for the blue/violet, and slightly below for the red). When the best foci are brought as close together as possible by a slight strengthening of the positive lens power (second plot from left), the paraxial foci spread wider, with paraxial foci in short wavelengths shifting at a greater rate than those in longer wavelengths.

And two plots at right show glass combination (early AP non-ED triplet) having significantly larger RPD differential in the violet g-line (Pg,F) than for the e-line (PF,e), thus having paraxial focus located significantly farther away from the common C/F focus than the e-line. When best foci of the most significant visual wavelengths are brought close together, there's a very small secondary spectrum residual for the e vs. F and C lines, but the best focus of the violet g-line - at about 0.7 zone - is left hanging out. Since secondary spherical is relatively small, good approximation of the magnitude of error in the g-line is obtained from the best focus P-V wavefront error relation for primary spherical, W=L/64F2 (L being the longitudinal aberration, and F the focal ratio). Here, L=0.64mm and W=0.000157mm, or 0.36 waves in units of 436nm wavelength. And since the best e-line focus is about 1.55 farther from best g-line focus than its paraxial focus, where the P-V error is four times larger, or 1.44 wave, the g-line error at the best e-line focus is about that much larger, 1.55 times 1.44, or 2.2 waves.

In all, well corrected lens objective requires glasses that are:
- good RPD match (for corrected longitudinal chromatism),
- good Abbe differential match (for low level spherochromatism and higher-order spherical), and
- good match in their refractive power (for low higher order spherical arising from imbalance in
higher-order spherical contribution from strongly curved surfaces).

There is no incentive to design semi-apo objective secondary-spectrum-wise using low-dispersion glass, other than for fast doublets needing more of Abbe differential to control spherochromatism. Slow and very slow doublets with significantly lower secondary spectrum than standard achromats can be designed combining common glasses (in general, those grouped around BK7-KF3 line, with somewhat "abnormal" glasses, like short flints (KZFS) and lanthanum glasses, shifted somewhat to the right, or phosphate crown (PK/PSK) glasses, shifted somewhat to the left. These somewhat abnormal glasses are generally more expensive than common glasses, and the degree of secondary spectrum reduction obtainable with them generally is not commensurate to the increased cost. All these glasses, common and somewhat abnormal, have relatively small respective Abbe differentials, hence can be used in a doublet form only for very slow objectives. Even f/12-f/15 objectives of this type generally require triplet form.

Relatively small secondary spectrum reduction is possible by optimizing common-glass combinations. For instance replacing BK7 crown with BAK2 in combination with F2 flint would reduce secondary spectrum by nearly 10%. However, that is paid for by ~25% glass cost increase. More substantial secondary spectrum reductions are possible with the second element being somewhat abnormal glass but, as mentioned, such combinations are suitable only for very slow doublets, or still fairly slow triplet objectives. In the triplet form, correction can be at the apo level, or quite close, except for the outer portion of the visual range, typically violet. An example are early Astro-Physics triplets made around short flint supply obtained from NASA (similar to KZFS1). Nowadays, most short flint glasses are available only as special melts, which makes them very expensive; noted exception is Schott KZFSN4, but it is still relatively expensive (about five times the BK7 price) and suitable only for relatively slow triplet objectives (as RPD diagram above shows, it has too high relative partial dispersion to be a good match for minimizing secondary spectrum with low and extra-low-dispersion glasses).

Following page brings some examples of lens objectives with semi-apochromatic and apochromatic correction.

◄ 9.1 Refracting telescope objective: Achromats ▐ 9.2.1. Semi-apo and apo objectives: examples ►

Home | Comments