3.3. CONICS AND optical ABERRATIONS

PAGE HIGHLIGHTS
• Types of conic surfaces • Eccentricity • Schwarzschild constant (conic)

Telescope aberrations can be divided in two main groups: (1) those intrinsic to optical elements in their proper alignment, and (2) aberrations induced by some external factor. This division is not exclusive; most major aberrations can be caused by both, intrinsic surface properties and misalignment or thermal factors. Rather, its purpose is to identify and relate aberrations according to their origin.

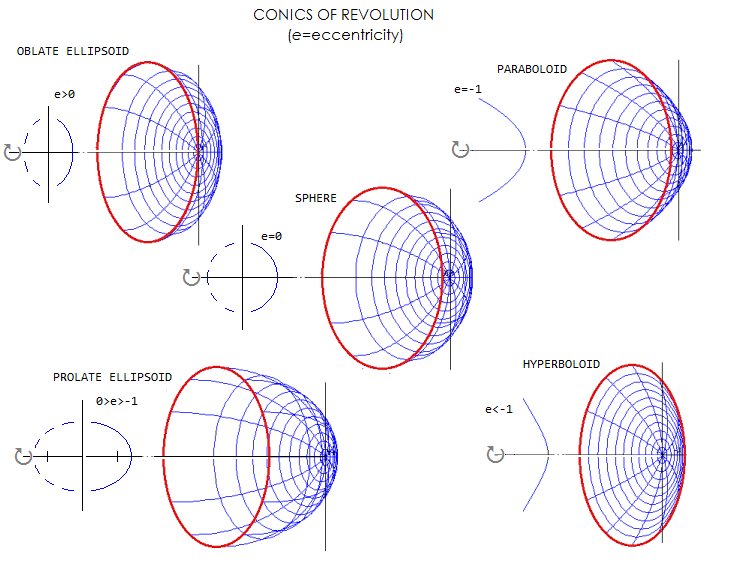
Among the aberrations caused by intrinsic properties of optical elements, most important are those characteristic of a conic surface of revolution in monochromatic (single wavelength) light. This surface is formed by rotation of a conic section around its axis of symmetry. Conic section is a curved line formed by the intersection points of a cone surface and a plane, as illustrated to the left. Following text describes conic surfaces in the context of their optical properties.

While all conic surfaces of revolution have perfect radial symmetry, that alone does not enable them to form perfect wavefronts. For this to happen, a surface must have specific form determined by both, its optical properties (index of reflection or refraction) and form of the incoming wavefront.

For instance, spherical reflecting surface will form a perfect spherical wavefront if the object is placed at the mirror center of curvature (obviously, the emitted wavefront, the surface and the reflected wavefront all coincide at the surface). However, as the object distance increases and the wavefront flattens, spherical surface advances wavefront points toward the edges more than those toward the center. As a result, the reflected wavefront is aberrated, curving in more strongly toward the edges than its perfect reference sphere. For object at infinity, the incoming wavefront is practically flat, and the extent of aberration reaches its maximum. Thus, a surface curving less toward the edges - a paraboloid - is needed to form a perfect spherical wavefront. For intermediate object distances, the "perfect" surface is an appropriate prolate ellipsoid.

3.3.1. Conic sections, geometric properties

In other words, for any reflecting conic surface there is a single pair of conjugate points (i.e. object and image locations) that will produce perfect axial image (such surface is called Cartesian reflecting surface). We'll call these two points (conic) specific conjugates, or specific/geometric foci. This pair of points is, in fact, what optically defines the conic curve, as a set of points for which a sum of the geometric (straight line) separation from the two specific conjugates (foci) is constant. Obviously, that is the condition for zero aberrations, since this geometric separation, assuming homogeneous medium, is proportional to the optical path length (OPL).

Note that geometric focus of a conic surface is different from its Gaussian focus, which is determined by the focal length - i.e. radius of curvature - of a surface, and independent of the conic.

For the sphere, the geometric foci coincide at its center of curvature; for parabola, one is at the Gaussian focus, and the other at infinity; for hyperbola, one is on the opposite side of surface and the other one is inside the focal point (this merely means that it is free from spherical aberration for object distance smaller than its focal length, or for converging incoming beam).

For prolate ellipse - the one with horizontal axis longer than vertical axis - specific foci lie at the longer (horizontal axis), equally separated from the center point (F1 and F2 in FIG. 23). And for oblate ellipse, the two spherical aberration-free conjugates, or foci, are also on the longer axis, which is this time vertical (note that the ellipse here is categorized as oblate or prolate based on its form around the optical axis, which is horizontal; when placed in a coordinate system and categorized with respect to the vertical axis, ellipse is oblate when flattened vertically, and prolate when vertically extended).

FIGURE 23: Conic sections are curves formed at the intersection of a plane and the surface of a circular cone. A cross-section parallel with the cone base produces a circle, symmetrical around its center point (O), while other cross-section angles produce ellipses, parabola and hyperbolas. The later group of conic sections is defined by their two specific conjugates, or geometric foci (F1, F2, with the near focus for parabola coinciding with the Gaussian infinity focus common to all conics with a given vertex
radius R). All rays coming from one specific focus pass through the other after reflection from a conic. The foci are positioned symmetrically around the center point (O, OP for the sphere and prolate ellipse shown, respectively). Deviation of a particular conic from the circular form is numerically expressed as eccentricity ε, which can by defined as a ratio of the inter-focus separation 2s=S and optical path length (OPL) between the foci via conic point C. The alternative - and more commonly used - measure is the conic constant K=-ε2. Numerical values of the conic constant are K=0 for sphere, -1<K<0 prolate ellipsoids, K=-1 paraboloid, K<-1 hyperboloids and 0<K for oblate ellipsoids. Each conic produces perfect axial wavefront for object located at one of its two geometric foci. Note that the eccentricity value shown for the oblate ellipse εt=0.5 is its actual eccentricity, derived from its center-to-focus separation vs. longer (vertical) semi-axis, and identical to its directrix-defined eccentricity. Commonly used eccentricity value ε for oblate ellipse is derived using its shorter (horizontal) semi-axis in the denominator, thus larger by a factor 1/(1-εt2)1/2 nominally; hence, ε=εt/(1-εt2)1/2, and εt2=ε2/(1+ε2). The common eccentricity form ε of the prolate ellipse - which we will term relative eccentricity - is needed for the ellipse equation, defining the conic's line, and the relations defining the length of their semi-axes a and b, but it is not a true, directrix-defined eccentricity of the oblate ellipse.

Rotating conic section 360° around its axis of symmetry produces a conic surface of revolution centered around its vertex: rotating the circle produces sphere, oblate ellipse produces oblate ellipsoid, prolate ellipse produces prolate ellipsoid, parabola paraboloid, and hyperbola hyperboloid.

The main parameters of these surfaces are given in the table below, followed by more detailed description.

CONIC	ECCENTRICITY (ε)	ε2	CONIC CONSTANT K=-ε2	NEAR FOCUS LOCATION @ R/(1+ε) from vertex,	FAR FOCUS LOCATION @ R/(1-ε) from vertex
Circle, a=b=R	0	0	0	coinciding at the center of curvature (COC)
Oblate ellipsoid*, a<b	>0 (0<εt<1)	-	>1 (0<K<1)	foci symmetrical around line perpendicular to axis, the line being inside COC at R/(1-ε2)1/2 from vertex
Prolate ellipsoid, a>b	0<ε<1	+	-1<K<0	between COC and Gaussian focus	outside COC
Paraboloid, a,b=∞	1	+	-1	Gaussian focus	infinity
Hyperboloid, \|a\|>\|b\| for ε2<2 \|a\|=\|b\| for ε2=2 \|a\|<\|b\| for ε2>2	>1	+	<-1	inside Gaussian focus	opposite to surface orientation

TABLE 1: Characteristics of the five main types of conic surfaces.
*True eccentricity/conic is in brackets; conic constant is given as positive, to differentiate between the two types of ellipsoidal surface; oblate ellipse's eccentricity value ε used in the ellipse function (not a true eccentricity εt), derived from the conic function based center-to-focus value c2=a2-b2, is an imaginary number of the negative sign when squared.)

EXAMPLE: Conic parameters for selected eccentricity values ε (εt and ε for oblate ellipse) for a concave mirror of radius R.

	OBLATE ELLIPSE, ε(εt)		CIRCLE	PROLATE ELLIPSE		PARABOLA	HYPERBOLA
ε	2.065(0.9)	0.577(0.5)	0	0.5	0.9	1	1.5	2
K	4.26	0.33	0	-0.25	-0.81	-1	-2.25	- 4
a	0.19R*	0.75R*	R	1.33R	5.26R	∞	0.8R	0.33R
b/a	1.345*	1.118*	1	0.87	0.44	0	1.12	1.73
near focus	0.55R**	0.8R**	R	0.67R	0.53R	R/2	R/2.5	R/3
far focus	0.55R**	0.8R**	R	2R	10R	∞	-2R	-R
uses ε, ε2<0 for oblate ellipse * to the foci-containing vertical line

In terms of conics' shape, for given vertex radius, oblate ellipses are most strongly curving away from the vertex (center). As their vertical foci converge closer, oblate ellipse becomes less strongly curved, converging to a circle when its foci merge in a single point. As the center of a circle separates into a pair of points on horizontal axis, they define the next less strongly curved conic, prolate ellipse. Further increase in separation of the two foci results in still less strongly curved conics: parabola, for which the farther away focus lies at infinity, and hyperbola, whose far focus is beyond infinity - at the opposite side of conic's vertex.

The measure of how strongly curved is a conic section is its eccentricity (ε). In optical terms, it can be expressed as the ratio of its inter-focal separation to the optical path length (OPL) from one specific focus to another, via any point of a conic (any ray originating at one of the two foci is reflected to the other one). Since both parameters are constant for given conic shape, so is its eccentricity (note that eccentricity of conic sections is usually expressed in geometric terms - as the ratio of a conic's point distance from its near focus to that point's distance to a fixed straight line, called directrix - but defining it in optical terms is more appropriate here).

For oblate ellipse, the inter-focus separation is finite, and ranges from approaching zero to approaching the optical path length between the foci, via point belonging to a conic section. Thus, its true eccentricity range is 0<εt<1, same as in prolate ellipse. Note that the use of true eccentricity figure, given as a ratio of inter-focus separation vs. ellipse axis that contains them, is uncommon; usually, the eccentricity of oblate ellipse is expressed in the same manner as for prolate ellipse, that is, as the ratio of its inter-focus separation vs. horizontal axis. This, relative eccentricity, doesn't reflect true, directrix defined value, thus oblate ellipse with identical relative (commonly used) eccentricity value doesn't have identical axial proportions to those of prolate ellipse of the same eccentricity value. Relative eccentricity ε of the oblate ellipse is merely the one determined by the ellipse function (Eq. 4) as the value describing it as a line in a coordinate system that is rotated by 90° (with the center shifted to the vertex of its short axis) with respect to its directrix.

On the other hand, true eccentricity of oblate ellipse identical to the eccentricity value of prolate ellipse implies identical axial proportions of the two: their longer vs. shorter axis ratio is identical, with the oblate ellipse only being smaller for given vertex radius, by a ratio (1-εo2)1/2/(1-εp2), where εo is the oblate ellipse eccentricity εo=ε (εo2<0) and εo the prolate ellipse eccentricity.

Thus, to convert from the true oblate ellipse eccentricity εt to the relative eccentricity ε, the former is to be multiplied by the ratio of longer vs. shorter axis of the oblate ellipse. This ratio is given by (1-εt2)1/2/(1-εt2), or 1/(1-εt2)1/2. For instance, a common eccentricity equivalent for true oblate ellipse eccentricity value εt=0.95 would be ε=1.93. Conversely, εt2=ε2/(1+ε2).

For the circle, the inter-focus separation is zero, and so is its eccentricity.

For prolate ellipse, the inter-focus separation is finite, always smaller than the OPL; thus, its eccentricity range is 0<ε<1.

Inter-focus separation for parabola, with one specific focus at infinity is infinity, and so is the OPL; thus its eccentricity equals 1.

Finally, for hyperbola, with one specific conjugate (focus) located inside its Gaussian focus, and the other, imaginary, on the opposite (positive) side of the conic's vertex, the inter-focus separation, which is positive, is always greater than the OPL. Here, the inter-focus separation is identical to the OPL geometrically, but is numerically smaller, being given by a sum of the larger, positive portion measured from the surface to the imaginary specific focus to the right, and smaller negative portion measured from the surface to the real specific focus located to the left of the vertex, inside the Gaussian focus.

Conic shape is commonly expressed as the conic, or Schwarzschild constant, defined as K=-e2. Since the eccentricity e is a positive number for all conics but oblate ellipses, the corresponding conic is negative for prolate ellipses, parabola, and hyperbolas. It is positive for oblate ellipses (this originates from mathematical formalism, defining ellipse center-to-focus separation s with s2=a2-b2, a and b being the horizontal and vertical semi-axis, respectively; since in oblate ellipses the latter is longer, their s2 is a negative value, and ε2= s2/a2.

Denoting the inter-focus separation as S, and the optical path length from one specific focus to a conic point and to the other specific focus as OPL, the eccentricity is given by ε=S/OPL. It defines the conic section as:

or (1+K)x2-2Rx+y2=0, with R being the vertex radius of curvature, and x and y being the horizontal and vertical coordinate, respectively. This relation defines the sag x of a conic surface as:

Specific near focus distance from the conic's vertex, in terms of the vertex radius of curvature R, is given by:

That gives L1=R for sphere, L1=R/2 for parabola, and intermediate values for prolate ellipses. For hyperbolas, L1=R/(1-ε). Near focus distance is smaller than R/2 for hyperbolas and oblate ellipses. Note that the latter are a special case, in that their specific foci are not located on the axis, rather on a straight line perpendicular to it. Separation from the axis, and the conic vertex here is equal for both foci. The vertex-to-perpendicular-line separation is R/(1-ε2), with ε2 being, by definition, negative for oblate ellipses, and the vertex-to-focus separation is R/(1-ε2)1/2.

Far focus distance from the vertex, also not applying to oblate ellipses and hyperbolas, is:

For hyperbolas, it is L2=R/(1+ε).

The inter-focus separation S, measured from the near focus with a conic oriented to the left, for all conics except oblate ellipses is given by:

For oblate ellipses, the inter-focus separation, after substitutions in s2=a2-b2 and taking absolute value for ε2 under the square root, is given by:

where the eccentricity ε is positive, and ε2, as before, negative. This gives S=0 for the circle, S=-∞ for parabola, -∞<S<0 for prolate ellipse, 0<S<0.5R for oblate ellipse (inter-focal separation here reaches maximum of 0.5R for the eccentricity ε=1, decreasing for both, higher and lower values of ε), and 0>S>∞ for hyperbolas.

The optical path length (OPL) between the two specific foci, via point on the conic, is given by:

for all conics except oblate ellipse, for which OPLo=2R/(1-ε2)1/2 = 2R/(1+K)1/2.

This gives OPL=2R for a sphere, OPL=-∞ for parabola, -∞<OPL<2R for prolate ellipses, 2R<OPL<0 for oblate ellipses, and 0<OPL<∞ for hyperbolas (note that Eq. 4.3 gives the geometric OPL; nominal OPL for hyperbolas, determining their eccentricity, is smaller - and of positive sign - given by the difference between the larger positive vertex-to-far and smaller negative vertex-to-near specific focus).

The eccentricity expressed as ε=S/OPL is, therefore, of a positive sign for all conic types (zero fo circle).

The OPL as given by Eq. 4.4 is identical to the length of the longer axis of either prolate or oblate ellipses.

An alternative set of relations for ellipses is based on the vertex radius of curvature R, horizontal semi-axis a and vertical semi-axis b, as shown in FIG 23. With a=R/(1-ε2) and b=R/(1-ε2)1/2, the eccentricity is given by ε2=1-(b/a)2, and the vertex radius of curvature R=b2/a.

◄ 3.2. Ray (geometric) aberrations ▐ 3.3.2. Aberrations of the conic surface ►

Home | Comments