|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
5.2. Low-level turbulence, tube currents...
▐
6. EFFECTS OF WAVEFRONT ABERRATIONS
► 5.3. Optical misalignment: tilt, decenter and despaceFor best performance, optical surfaces of a telescope have to be in their optimum alignment. Any deviation from the optimum position - be it tilt, decenter or despace - will negatively affect wavefront accuracy (FIG. 90). Degree of sensitivity to misalignment vary with the design and system properties. In general, the more optical surfaces and the more strongly curved they are, the greater misalignment sensitivity. More specific consequences of misalignment are addressed with each particular telescope type.
Probably the most common miscollimation error is coma induced by misaligned primary and secondary mirror. With a flat secondary mirror (Newtonian) it simply shifts the axis of the primary away from the eyepiece axis, bringing a portion of the image affected by (existing) off-axis aberrations to the field center. In a two-mirror system it creates coma where there was none before. As can be grasped from the illustrations (FIG. 53, left and center), the misaligned surface induces the same amount of error to the wavefront regardless of its inclination. Hence this coma is invariant to field angle; in a coma-free system, it affects the entire field equally, while in a system with existing (inherent) coma, it is intact only in the field center, while either lessening - or adding to - the existing coma in the rest of the field.
Taking as an example a common 100mm f/10 achromat, its two lenses
can be decentered, tilted and/or despaced. Despace induces only spherical
aberration (widening the gap undercorrection, and vice versa). Tilt
and decenter will induce all-field coma, but will also affect lateral
color error (larger tilt/decenter values will also induce image tilt,
but they are not possible in a functional lens cell).
Decentering either lens alone induces more than 1/2 wave P-V of all-field
coma, as well as all-field lateral color error, with F and C line
separation nearly equaling e-line Airy disc diameter. Tilting either
lens by 0.05° induces near 0.6 waves P-V of all-field coma, and
about half Airy disc F/C separation. If both lenses are tilted, the
effect is negligible. If the rear lens is tilted as much but in
opposite direction, the coma nearly doubles, but lateral color error
is cut in half. The magnitude of aberration induced is commensurate
to the nominal misalignment, and its sign changes with the sign of
misalignment (same sign of tilt and decenter of the negative lens induce coma of
opposite sign to that of the positive lens).
This exercise shows that even the common f/10 achromat
requires fairly tightly aligned lenses in order to avoid significant
aberrations induced. This is raised to another level with apo doublets
and triplets. For instance, decentering one lens by 0.25mm in the
Takahashi FC100DZ f/8 doublet
induces 2.7 waves P-V of coma, and with faster doublets it can be up to 2-3
times as much. That same decenter in a 100mm f/6.5 BSC7/FCD100/BSC7
triplet (middle element) would induce 4.2 waves P-V of coma,
while 0.05° tilt of that same element would induce 1.2 waves P-V
of coma.
The enormously high surface accuracy
requirements for optical surfaces of a telescope results in high
sensitivity to even slight changes induced by external forces. Such
forces commonly are: (1) thermal
expansion and contraction, (2) pressure by the mounting elements, and (3) force of gravity.
Thermal expansion and contraction
causes surface deformities due to their uneven rate within the body of
an optical element. Given material homogeneity and thermal properties,
it becomes more of a problem as the volume of an element increases, and
as the mass distribution gets more uneven. Relatively small differences
in the temperature can cause significant surface deformations and
resulting wavefront error. The dominant aberration induced is
usually spherical and/or edge defect error, but other, more or less
random forms of wavefront deformation are frequent. The only cure to it is to get optical elements to a
thermal near-equilibrium with the surrounding air.
In general, mirrors are significantly more affected by thermal
expansion/contraction than lenses. This is due to the fact that
deviation at the reflective surface causes change in the wavefront
larger by a factor of (n-1)/2 than the same nominal deviation at the
lens surface, n being the lens refractive index (also due to
mirrors having typically significantly thicker edge for given diameter,
both nominally and relative to the center thickness). The usual scenario
is a telescope - including its optical components - warmer than
surrounding air for more or less extended period of time (depends of
telescope size, thermal characteristics of the optics and mechanics, and
passive/natural vs. active/fan cooling).
Once the entire objective cools down to a new temperature, the only
consequence is slight reduction in focal length, caused by the slight
reduction in its size and proportional to it. With the linear
coefficient of thermal expansion for standard optical glasses of
~0.000006/°C, the change in focal length for as much as 10°C change in
the temperature of the objective is still only ~f/17,000,
f being the focal length (it
is usually smaller than reduction of tube/structure length caused by
cooling). In the process, however, surface deformations caused
by thermally caused shrinkage or expansion can create wavefront
aberrations, especially when portions of the optical element (front vs.
back, top vs. bottom, center vs. edges) are cooling or warming up at
different rates (FIG. 91).
The general form of surface deformation is opposite for contraction vs.
expansion. In a concave mirror, contraction will induce overcorrection.
Quantifying the error involves extensive calculation with material,
dimensions, temperatures and present factors other than the optical
element itself influencing the process of thermal transfer specified.
For a rough approximation of the error level in the scenario with uneven
rate of cool down for the front and rear, an arbitrary assumption can be
made that contraction of the cooler, front side, and partial contraction
of the circumference wall area, have brought the edge point E of
the wormer shape to the point H of the cooler shape, with the
length GH being 1/2 of the full contraction along the edge
(width-wise parallel to axis).
For a mirror, with relatively small axial vs. edge thickness difference,
arbitrarily assuming axial contraction 1/2 of the edge contraction, the
edge contraction versus center is by ~τT/2
greater, with τ being the glass
thermal expansion coefficient (linear) and T the edge thickness.
This contraction differential equals the peak surface deviation from its
original form. With the thermal expansion coefficient being for the
linear expansion per 1°C, this simple relation gives an idea of the
level of peak (edge) surface deviation for every 1°C differential
between the front and back of the mirror.
With the coefficient of expansion for plate glass τ~0.0000085/°C,
the edge vs. center surface deviation is ~1/5 wave (for 550nm wavelength) edge surface error for every inch of
mirror thickness, doubling in the wavefront. Pyrex, with about 2.5 times
smaller thermal expansion coefficient, will have proportionally smaller
deformation. Due to the deviation increasing from center toward the edge, it
produces wavefront deviation generally resembling spherical aberration
and/or defocus. For an actual surface
error, the wavefront error is probably somewhat smaller than double as
much - possibly significantly - due to refocusing (i.e. better fit of
the deformed wavefront to a reference sphere of slightly longer radius).
The RMS error may be lower than for ordinary spherical aberration even
before refocusing, since it seems possible that the wavefront could be
comparatively less affected away from the edge area, hence more
resembling the higher-order terms, affecting relatively smaller
wavefront area. In the scenario
where both, front and rear of a mirror are similarly exposed to cooler
air, the error is likely to be greater, due to more rapid cooldown of
the entire circumference area.
Pressure from
mounting elements
usually causes some form of astigmatism, due to
the typically
radially symmetric
distribution of the points of support and/or retaining. Typical pinching
pressure, for instance, induces trefoil (under "pinching") - a three-winged form of
astigmatism, quickly revealing itself in the appearance of diffraction
pattern. Mounting pressure can result from thermal expansion of
optical elements and/or mechanical structure, which is one more reason
why optical elements should be left slightly loose within mechanical
structures holding them.
Gravitational force tends to
deform larger pieces of glass, especially if they are relatively thin.
The form of deformation depends on the position angle, as well as on the
support points distribution and level. While the error induced by gravitational
force is
usually low to very low, it can become significant in larger diameters,
especially large thin mirrors. Proper support structure here can be
critical. Popular free software,
PLOP, evaluates the
error induced by gravitational force to a mirror on mirror cell support
points. Below is shown how it evaluates effect of mirror support on mirror surface,
for 200mm and 400mm mirror diameter, and 1/6 and 1/10 thickness-to diameter ratio (error
values are those calculated with Z88 which are, acorrding to Lewis, more accurate).
Mirror material is Pyrex, which is somewhat better in this respect than plate glass.
The shown support point distribution is program-optimized for the lowest surface RMS error. Added
error is negligible for small deviations from the optimal distribution. The error
doubles in the wavefront, so, for instance, a 20mm thick 200mm f/6 mirror on 3-point support
will have 0.000057mm RMS wavefront error, or 0.01 wave RMS for 0.00055mm wavelength, of
support-induced deformation. It still corresponds to as little as 0.996 Strehl degradation factor
(from 1-39.5RMS2). Mirror focal ratio - i.e. mirror depth - has a small, generally
negligible effect.
Common characteristic of induced
telescope aberrations is that they do not have pre-determined level.
Unlike the aberrations inherent to the optical set, they vary with the user, telescope and the circumstance. The effect on
image quality is directly related to the RMS wavefront error they cause,
which is often times hard to determine. Partly due to
this elusiveness, they are, in general, less well known of, and taken
less seriously than intrinsic telescope aberrations. However, there is no
difference in the effect of aberration, regardless of its origin.
Aberrations induced to a near-perfect optics can make it perform as a
third-grade system. Thus, knowledge and control of induced
telescope aberrations are unavoidable part of the proper routine of using
a telescope.
◄
5.2. Low-level turbulence, tube currents...
▐
6. EFFECTS OF WAVEFRONT ABERRATIONS
► |
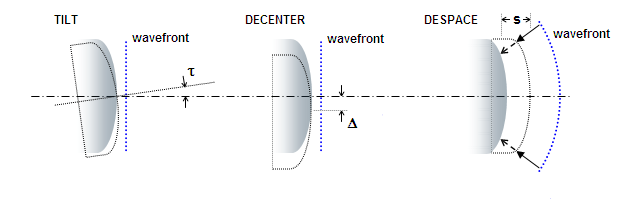 FIGURE 90:
Misaligned optical surface can be tilted, decentered, despaced, or any combination of the
three in
respect to its proper position. Tilt is expressed in angular form, while
decenter and despace are linear quantities. Tilt and decenter result in one
side of
the optical surface becoming closer to the wavefront than the other
one - a recipe for coma, which is by far the dominant resulting
aberration. Astigmatism, which results from wavefront's inclination
relative to the surface is small in comparison. Despace causes
mainly spherical aberration with converging or diverging wavefronts
- as shown to the right, result of the wavefront-to-surface
respective curvatures at the location of
reflection/refraction being different from those at the optimum
position.
FIGURE 90:
Misaligned optical surface can be tilted, decentered, despaced, or any combination of the
three in
respect to its proper position. Tilt is expressed in angular form, while
decenter and despace are linear quantities. Tilt and decenter result in one
side of
the optical surface becoming closer to the wavefront than the other
one - a recipe for coma, which is by far the dominant resulting
aberration. Astigmatism, which results from wavefront's inclination
relative to the surface is small in comparison. Despace causes
mainly spherical aberration with converging or diverging wavefronts
- as shown to the right, result of the wavefront-to-surface
respective curvatures at the location of
reflection/refraction being different from those at the optimum
position.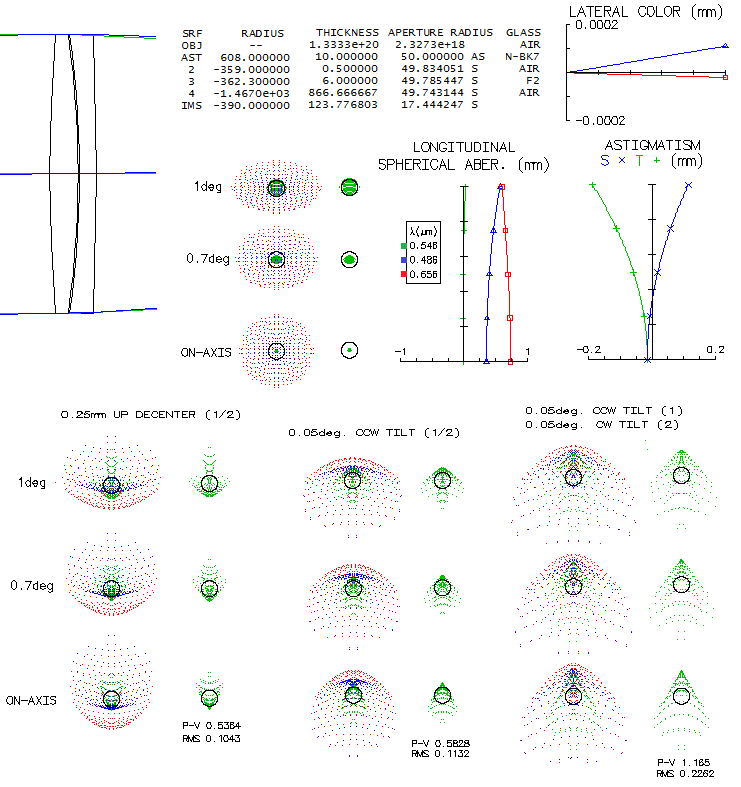
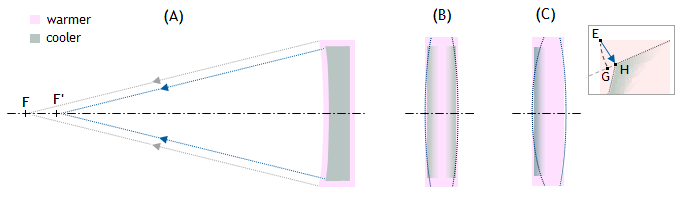 FIGURE 91: Effect of thermal
contraction on optical surface. Once the optical element has cooled down
entirely, it is slightly smaller, and the only consequence is slightly
shorter focal length (A). During the cooling process,
surfaces are stretched outward, due to the outer portion cooling (and
shrinking) at a faster rate than the inner mass (B). If one side
is cooling at a faster rate, it will also be more deformed (C).
The deformation weakens curvature of a concave surface toward the edge,
while strengthening the outer curvature of a convex surface. The inset
to the right gives a simplistic illustration of the mechanism causing the outer surface points
to be pulled
inward relative to the surface points closer to the center.
FIGURE 91: Effect of thermal
contraction on optical surface. Once the optical element has cooled down
entirely, it is slightly smaller, and the only consequence is slightly
shorter focal length (A). During the cooling process,
surfaces are stretched outward, due to the outer portion cooling (and
shrinking) at a faster rate than the inner mass (B). If one side
is cooling at a faster rate, it will also be more deformed (C).
The deformation weakens curvature of a concave surface toward the edge,
while strengthening the outer curvature of a convex surface. The inset
to the right gives a simplistic illustration of the mechanism causing the outer surface points
to be pulled
inward relative to the surface points closer to the center.
