10.2.3.3. MAKSUTOV-CASSEGRAIN TELESCOPE

• History • Types: Gregory and Rumak • Aspherising for a faster system • Field illumination
• Meniscus effect • Approximating meniscus radii • Mangin MCT • Veselkov MCT

Full-aperture meniscus corrector can be also used in various arrangements, including two-mirror systems, as described in Maksutov's extensive writings between 1941 and 1946. Nowadays, it is most often used in the Cassegrain configuration (FIG. 186), hence these systems are known as Maksutov-Cassegrain telescopes (MCT). The benefit of such an arrangement is - similarly to that in combination with the Schmidt corrector - greater flexibility in correcting primary aberrations than in an all-reflecting system. The usual meniscus orientation is concave to outside, when its coma is of opposite sign to that of the primary. It also generates more of higher-order spherical, but negligibly so unless the radii are strongly curved (in the Maksutov-Gregorian, where the secondary contribution for both, spherical and coma, is of opposite sign, both are a disadvantage, and it works better with the meniscus convex to outside; still, even with f/3 primary, a 200mm aperture has unappealing 1/20 wave RMS design limit for spherical aberration, and the reduction in it by aspherizing primary coming at a price of added coma). As it will be illustrated in this text, an MCT with separate secondary can be made corrected for all aberrations (correcting field curvature requires large secondary mirror) in an all-spherical arrangement. In addition, corrector's chromatism can be made nearly non-existent.

However, in compact systems with fast primary mirrors, the strongly curved surfaces of Maksutov corrector quickly begin to generate higher-order spherical aberration, which changes in proportion to the aperture and, approximately, with the fourth power of primary's relative aperture. It can only be corrected by applying aspheric surface term to either mirrors or the corrector - something too complex to be viable for amateur telescopes. While it varies somewhat with the specifics of corrector, acceptable optical quality in this respect doesn't extend significantly beyond a 6" f/3 primary level. Another option is to have the primary aspherised, which allows for weaker corrector, with reduced higher-order spherical aberration.

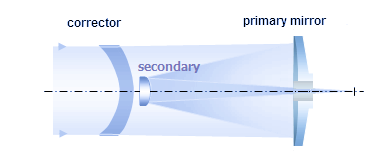
FIGURE 186: Maksutov-Cassegrain telescope optical elements. Meniscus corrector, which induces not only spherical, but also off-axis aberrations, offers greater flexibility in correcting system aberrations. As a result, Maksutov-Cassegrain can be made free from coma and astigmatism in a compact all-spherical arrangement. The weak point is strong higher-order spherical aberration with fast primary mirrors that require strongly curved corrector surfaces. It can not be corrected in an all-spherical arrangement. Secondary mirror can be either an aluminized spot on the rear of corrector, or a separate surface, which generally allows for better field quality.

First prototype of Maksutov's new telescope system was a Gregorian of 100mm aperture made according to his specs in 1941. With f/1.9 primary, an all spherical design had about 0.4 wave P-V of balanced 6th/4th order spherical (about 0.13 wave RMS) and worked acceptably well only up to about 40x magnification. As an oddity, it had focal plane a few mm in front of the primary, only allowing use of longer focal length eyepieces.

At about that time, being for a long time deeply involved in making school telescopes, Maksutov initiated a project of a small 70mm f/10 Cassegrain system serial production that will resume in continuity after the WW2. Many thousands of this telescope were made, known as Simplified School Telescope (УШТ abrreviation for its name in Russian). There is no official prescrition, but it can be re-engineered based on the specs from its brochure and some published direct measurements, as shown below (note that it is the optimized system; there are documents suggesting that the actual design initially had sub-optimal color correction - according to the prescriptions in Maksutov's papers, nearly 1/2 wave in the red and over 0.6 waves in the blue; also, actual measurements suggest that manufacturing errors could have been significant).

It had a small aperture and field of view, but was highly portable and went for what even in the Soviet Union was considered to be a low price (not long after Maksutov's death, it was discontinued, which suggests that it was his influence what kept such project going). The focal length may have been longer than stated, around f/12, or little more, at least for some; Yuri A. Klevtsov stated on a Russian forum that was the case with the unit he had back then). Early on, the eyepiece (Huygenian, possibly Kellner later on; it is possible that some chromatism was left in intentionally, since Huygenian eyepiece has longitudinal chromatism of opposite sign) was screwed on directly onto the rear side, with a very short back focal length (later vesions had it somewhat longer).

First published telescope arrangements in the U.S. that followed the 1941 introduction of a full-aperture meniscus corrector for spherical mirror was a pair of two-mirror Cassegrain systems - f/15 and f/23 - and Maksutov-type corrector by John Gregory. In it, the secondary was an aluminized spot at the back surface of the corrector. He published two 6-inch aperture designs in a 1957 issue of Sky and Telescope, raytraced below.

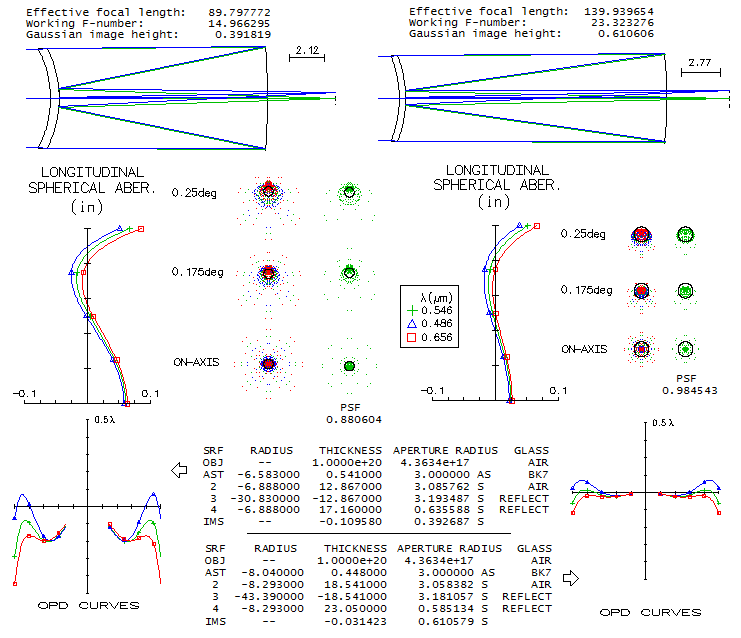
The f/15 design is pushing the limit of acceptable with its f/2.57 primary. The f/3.6 primary of the second design allows for the correction level that makes possible fabrication of a "sensibly perfect" telscope. However, both designes have longitudinal chromatism corrected by bringing together paraxial foci, while letting the more important, outer zones go to defocus. Making meniscus radii slightly weaker - 6.78 and 7.095" in the f/15 system - minimizes chromatic error, lowering it by about a half. But even in the original system, the F and C error is well below quarter wave P-V level if unoptimized, so it has relatively small effect. For today's standards, both designs have too short back focal length, which means that both would need to use a higher focal ratio (moving primary closer to the corrector to accomplish that would have little effect and, if needed, would be easy to offset by a very minor radius tweak). Otherwise, designes are a fine example of creating Maksutov system, which is not a simple task in any respect. Note that the spot diameter is 1.4" in the f/15, and 1.2" in the f/23.

At the time, Lawrence Braymer was already producing his famous-to-be Questar Maksutov-Cassegrain, a design very similar to Gregory's (in order to avoid patent infringement with a third party, Questars had - for about a decade - the aluminized spot placed at the front meniscus surface). As a later development, an arrangement with separate secondary was introduced.

Nowadays, both Gregory-type and the arrangement with separated secondary are being used in various forms. In general, separate secondary is preferred, since it gives additional degrees of freedom for correction of aberrations (FIG. 187).

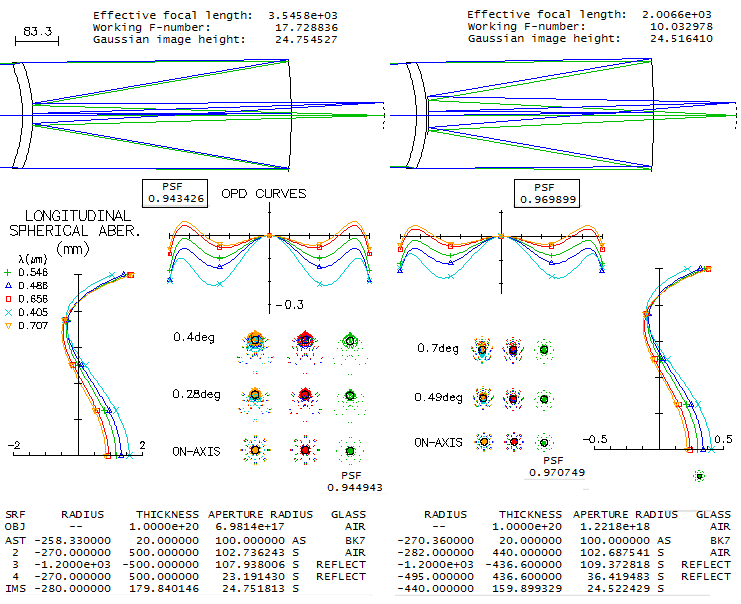
FIGURE 187: Two basic Maksutov-Cassegrain arrangements: (a) all-spherical with an aluminized spot on the back of corrector for the secondary (Gregory-style), and (b) with separated secondary. Due to design limitations imposed by the two surfaces of identical radius of curvature, the former has noticeably inferior off-axis performance: at 0.4° off-axis the wavefront error (best surface) is 0.18 wave RMS, mostly due to the coma, but also astigmatism. The design with separated secondary is highly corrected, with less than 0.06 wave RMS wavefront error at 0.7° off-axis (for identical field radius, the maximum that can fit to 2-inch barrel eyepiece). It is also better corrected axially (0.025 vs. 0.034 wave RMS), with lower field curvature due to both, lower astigmatism and larger secondary. Its minimum obstruction size is 0.30D, seemingly significantly larger than in the aluminized spot arrangement, but due to the conical baffle required by the latter, the actual difference is relatively small. Some lateral color error (LC) exists, but not enough to be intrusive visually. Both systems have very low chromatism, with their photopic polychromatic Strehl practically identical to the e-line Strehl.
Although known as all-spherical design, Maksutov-Cassegrain can also be made with aspheric surfaces. While either of the two main types above can have aspherized surface(s), in the amateur telescopes' arena it is usually the Gregory-style MCT, and it is usually the primary that is aspherized. The reason can be either making possible more compact, somewhat faster systems, or minimizing the higher-order spherical residual (or both, in larger apertures, such as Astro-Physics 10" MCT). Meade had its well known 7" f/15 version, and nowadays they are fairly common in the 4-8" aperture range, usually at about f/12.

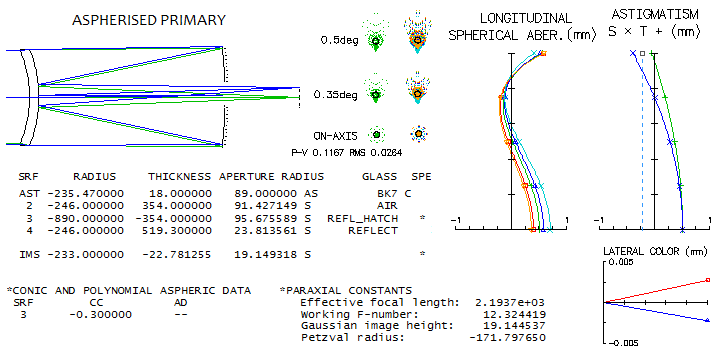
Aspherizing primary reduces the spherical aberration load on the meniscus, i.e. allows more relaxed radii. Since aspherizing primary introduces positive coma, and a standard Gregory-Maksutov has some residual negative (tail down) coma, this type of Gregory-Maksutov usually has residual positive coma, with the degree of aspherization limited by the level of acceptable coma. System above, with a -0.3 conic on the f/2.5 primary, has it at the visually negligible level (linear field like f/8.4 paraboloid). Due to the more relaxed radii and shorter tube, lateral color error is also somewhat lower than in the Gregory-Maksutov above, despite its slower primary. Balanced higher order spherical has 0.025 wave RMS design limit (comparable to 1/12 wave P-V of primary spherical). The level of chromatic correction is well illustrated by the violet g-line error: 0.032 wave RMS (0.96 Strehl). An f/15 system with f/2.8 primary, which should be close to the Meade's 7" GMT in that respect, with the same -0.3 conic on the primary would have less than 2/3 of the coma of this system (linear field), and an equivalent of 1/20 wave P-V of primary spherical aberration axial design limit. There would be no need for significantly more aspherized primary, and it is all but certain that it is nowhere close to parabolic, as some speculate, since such system can't be made functional.

By manipulating corrector thickness with a conic on the primary, a compact, relatively fast systems free of coma can be produced. Taking for example the more common, smaller MCT, like Celestron 127mm f/12, here's what it would look like with the standard corrector thickness (left) and thickness needed to correct coma (right).

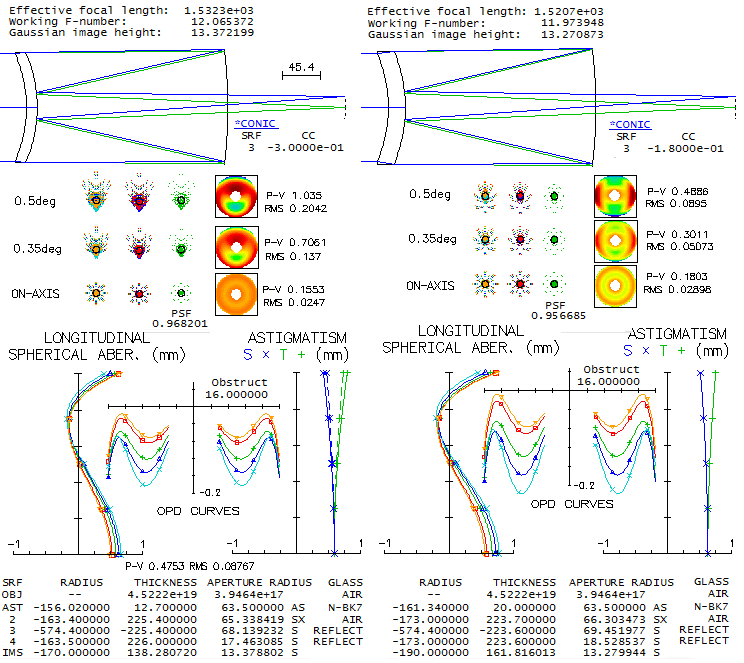
Due to the -0.33 primary conic making possible more relaxed radii, as fast as f/2.26 primary can be used (can't be significantly slower for the f/12 final focal ratio). Astigmatism is low (dashed on the astigmatism graph with 0.25D central obstruction with the solid line representing the same system w/o obstruction; actual obstruction is, due to the conical baffle around it, around 0.3D), according to the graph 0.41 wave P-V at 0.5° off axis. However, this strong conic turns the original negative (tip up) coma into positive. It is still low, with the 5mm "difraction-limited" (0.80 Strehl) field radius coresponding to f/7.8 paraboloid. E-line design limit is nearly 0.97 Strehl and, when the colors are optimally wrapped up, as shown, the polychromatic (photopic) Strehl is practically identical to it. In order to correct for coma, a lower primary conic is needed, and that requires thicker meniscus, which generally requires weaker radii, hence lower conic as well. The thickness needed to correct for coma here is about 20mm, with the resulting system having a slightly worse e-line design limit (despite somewhat weaker radii, due to its marginal ray at the primary being little higher). But it has better field correction and a significantly more generous back focal length.

One interesting aspect is the size of illuminated field. Taking the standard thicknes meniscus, and 27mm rear baffle tube opening, assuming it is at 100mm in front of the final image gives following result.

At 0.5° field radius, slightly smaller linearly than the baffle opening radius, vignetting is already present, but entirely negligible. At 0.6° it is still acceptable, but at 0.7° is barely passable (taking that one magnitude illumination drop is the acceptable limit for field edge, visually). That implies that the size of visually well illuminated field is about 1/3 larger than the baffle tube opening. In this case, about 18mm, or nearly 0.7 degrees true field (apparent field gets enlarged or reduced according to the eyepiece distortion level). Note that this ignores vignetting at the secondary and the baffle tube front opening; the former is generally negligible, but the latter is likely to be significant (see C9.25 baffling), although it is vignetting at the rear baffle opening which ultimately determines the size of usable field. This implies that this 5-inch Maksutov-Cassegrain does have illuminated field large enough to use 2" eyepieces, although those with the widest field stops will be severely vignetted close to field edge.

As described in the previous section, full-aperture meniscus corrector has properties making it quite complex optically. Part of it is due to its steeply curved surfaces, generating significant amount of higher-order aberrations. It is a thick lens, requiring more complex expressions for accurate assessment. Also, its relatively strong power makes system properties - including spherical aberration level - dependant on its location relative to the mirror. In two-mirror systems, this only becomes more complicated with the secondary mirror added. As a result, the path to defining a working system of this kind is fairly complicated, and can not be expressed with reasonably small set of equations.

With the arrangement with an aluminized spot for the secondary, needed secondary curvature for desired focus location determines back radius of the corrector, thus the only variable is corrector thickness and, to that extent, the front radius. The secondary curvature itself is determined by the properties of primary, which in turn are known only with the corrector properties specified. However, there is a typical level of the effect of the corrector on the primary, which can be used to obtain better initial approximation of needed system properties (FIG. 188).

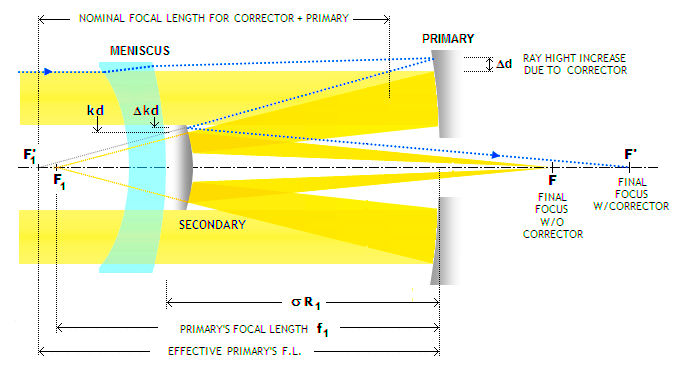
FIGURE 188: Effect of placing full-aperture meniscus corrector in a two-mirror system (dotted blue). Being thicker toward the edges, meniscus delays outer portions of the flat incoming wavefront more, changing its form into convex toward the primary. As a result, the outer rays diverge, as if coming from an object placed at meniscus' focal point (in terms of lens power, the meniscus is a negative lens). Due to the aperture stop being displaced from the primary, ray height at the primary is greater than at the first corrector surface (aperture opening), making the primary's optical radius larger. It also focuses (F1') farther away than without corrector in place (F1). Ray height on the secondary also increases from kd (k being the height in units of the aperture radius d) to (k+Δ)d. Since the corrector causes primary mirror to form its image farther away from the secondary, it re-images it at a greater distance from its surface, shifting the final focus F' farther out. Changes in the ray/wavefront geometry resulting from corrector's power change aberration contributions of the two mirrors. Typical ray height increase on the primary due to corrector's power is 4%-5%, and primary's effective focal ratio F is reduced by nearly 0.1 (which is reflected in the slightly shorter nominal focal length for the corrector and primary combined). These quantities help in the initial estimate of needed properties of the secondary and the corrector for given primary mirror.

Meniscus corrector for an MCT can be closely approximated based on Eq. 128-128.1, for a single mirror system, corrected for spherical aberration induced by secondary mirror. The correction is determined by Eq. 154, and implemented by substituting [1/(1+s')1/3]R for R in Eq. 126. Since the relative (in units of spherical aberration on the primary) level of spherical aberration on the secondary, given by s' value, is typically around 1/3 (neglecting the minus sign, which merely indicates aberration opposite in sign to that of the primary), the front meniscus radius in an MCT is generally somewhat weaker than for the meniscus that would correct the aberration of the primary alone; rear radius is then calculated based on the front radius approximation, as given with Eq. 128.1.

Adjustment to the corrector in order to minimize chromatism and spherical aberration are generally as those described under this last equation.

As an example, let's take a 150mm f/10 Maksutov with separated secondary, 15mm thick corrector and f/3 primary. This relatively fast system requires larger secondary, so let it be 0.33 (marginal ray height of the axial cone at the secondary, un units of aperture radius) needed for 200mm back focal length. The relative value of s is given by (d2/d1)⁴/ρ³, where d1=1, d2 and ρ are the aperture radius (taken as unit), secondary's axial cone radius and ρ=R2/R1, the secondary's radius of curvature in units of the primary's, respectively. Since ρ=mk/(m-1), with k=d2/d1, and m the secondary magnification, it comes to ρ=0.47R1, or -423mm. That gives s'=0.114, or little less than 1/9 of the aberration at the primary. However, this assumes object at infinity for both mirrors. In order to calculate the actual s' it is necessary to adjust spherical aberration at the secondary by entering the object distance factor, given for spherical mirror by (1-2ψ)², where ψ is the reverse of object distance in units of the mirror focal length. We know that the object distance (image by the primary) is -150mm here, and the focal length is -211.5mm. This gives ψ=1.41, and the correction factor for the secondary's spherical aberration of 3.3. So the actual level of spherical aberration on the secondary is as many times higher, or s'=0.38 relative to the primary. With this, the effective mirror radius to correct is R1e=[1/(1+s')^1/3]R1, or 1.17R1. Using this value to obtain 0.9R" as the front meniscus radius approximation given by Eq.126, gives for the front meniscus radius C1=-206mm. The corresponding rear radius (Eq.127) is C2=-214.5. Image below shows this system before and after optimization. Considering that calculation doesn't take into account higher-order spherical, it is about as close as it gets.

In the Gregory-Maksutov, as mentioned, the additional constraint is that the secondary radius coincides with the rear corrector radius. For all spherical system, corrector radius needed to generate spherical aberration that will - combined with that of the secondary - cancel out spherical aberration of the primary is, in general, stronger than the secondary radius required for usable systems with mid-to-low secondary magnifications. When it is set equal, as in the Gregory-Maksutov, it will produce diverging beam unless pulled farther from the primary. Hence, secondary becomes both, more strogly curved and smaller. In order to have both, corrected spherical aberration and accessible final focus, Gregory-Maksutove typically requires secondary magnification larger than 5, most likely around 6 for the comfortable back focal length. Usable systems with lower secondary magnification would require aspherized primary, allowing for more relaxed corrector radii.

Because of the mentioned constraint, R2=C2, the latter being the rear corrector radius, the above calculation for meniscus radius can't be applied directly to Gregory-Maksutov: we don't know size of the secondary before we know the rear meniscus radius, and can't determine the latter without knowing the secondary size. The starting point is the empirical approximate minimum secondary magnification value of 6. So with the same f/3 primary the expected final f-ratio is around f/18. From the back focal length, BFL=(m+1)k-1 in units of primary's focal length, using m=6 determines value of k. In this case, BFL=200mm, or 0.444f1, so k=1.444/7=0.206. The corresponding value for ρ is ρ=mk/(m-1)=0.247, i.e. the secondary focal length f2=-222mm (note that this is not also the value for the rear meniscus radius yet, it is only needed for calculation; rear meniscus radius has to be obtained from the spherical aberration values). Now, with the relative spherical aberration at the secondary s=k⁴/r³=0.12 for object at infinity, and nearly twice bigger, or 0.233 when corrected for object distance, giving R1e=1.092R1. With 1.17R1 producing -206mm, the front meniscus radius here is C1=-192.3mm and the corresponding rear radius is C2=-200.8mm. Raytrace below shows that these numbers are again spot on chromatism-wise and quite close to the optimal values spherical aberration wise. Note that after adjusting C2 value the back focal length changes to 199.2mm, for the final f/19.5 system, i.e. 6.5 secondary magnification.

For a faster, more compact design, primary needs to be aspherized. Following the same path with f/2.6 primary - which with K=-0.2 conic (approx. the value cancelling out coma) has spherical aberration of f/2.8 - and 200mm BFL, we approximate k from BFL taking only fractionally smaller secondary magnification, say, 6 (most of the system f-ratio reduction comes from the faster primary). That gives BFL=0.51f1 (with the geometric f/2.6 primary), k=1.51/7=0.216, and ρ=0.26 (f2=-101mm), with the infinity s=0.124, and the actual s' nearly two times larger, or 0.24. That gives R1e=1.1R1, with the front meniscus radius approximated as 0.9R"=0.223R1. What still needs to be accounted for is the effect of conic, which lowers spherical aberration at the primary by 20% and, with spherical aberration changing inversely to the 3rd power of radius value, makes it effectively 0.9R"=0.24R1, or C1=-187.4mm. This determines the rear radius C2=-195.9mm. Raytrace below shows another system close to the optimum level, slightly closer in monochromatic correction, and slightly less so in the chromatic (radii need to be about 5mm weaker in order to optimally wrap up the colors). The final system f-ratio is f/15.8.

Two-mirror Maksutov system aberrations are addressed in more details in the following chapter. While fourth-order coefficients - in particular for spherical aberration - are not sufficiently accurate for determining final system properties, they are necessary for understanding system's properties.

MANGIN-MAKSUTOV-CASSEGRAIN

An interesting possibility is to have a Mangin mirror for the primary, i.e. to make it a positive meniscus with refraction at the front surface and a single reflection at the rear surface. The same can be done with the secondary by putting reflecting spot on the front meniscus side; the effect of the latter is near-negligible, but turning the primary into Mangin mirror allows for much more flexibility with respect to the meniscus radii, making possible a significant reduction in the higher-order spherical residual and faster systems for a given power of the reflective side of the primary. In other words, produces effects similar to those of aspherizing the primary.

As an example, image below shows a small 80mm aperture system with the reflective side of the primary corresponding to f/2.5 mirror. Size of central obstruction is approximated by the diameter of the secondary baffle opening, in this case taken as 28mm (35%). Back focal length is on the short side, but acceptable for this small system.

Overall, the output is quite similar to that of the standard MCT. In order to pinpoint the differences, a standard MCT with identical aperture and reflective surface radius of the primary is shown below. For similar back focal length, it is slower at f/14 vs. f/12.1 for the Mangin arrangement. It also requires somewhat smaller central obstruction, 23 vs. 28mm. Aberrations wise, the reflective side of Mangin mirror and its front side (mostly second refraction) induce roughly as much of spherical aberration and coma as the primary mirror in the standard MCT. Astigmatism in the Mangin arrangement is over 30% lower, but lateral color error is three times larger (lateral color coud be easily managed with a field lens, but that is an extra element which would make comparison less direct). Meniscus radii in the standard arrangement are somewhat stronger, resulting in a little more of the higher-order spherical residual (radii strengthening is necessary in order to bring the colors tightly together; if only spherical aberration would be minimized by making the front radius somewhat weaker, the defocus error for given meniscus thickness would have been about 1/2 wave in the red C line, and about 3/4 wave in the blue F line).

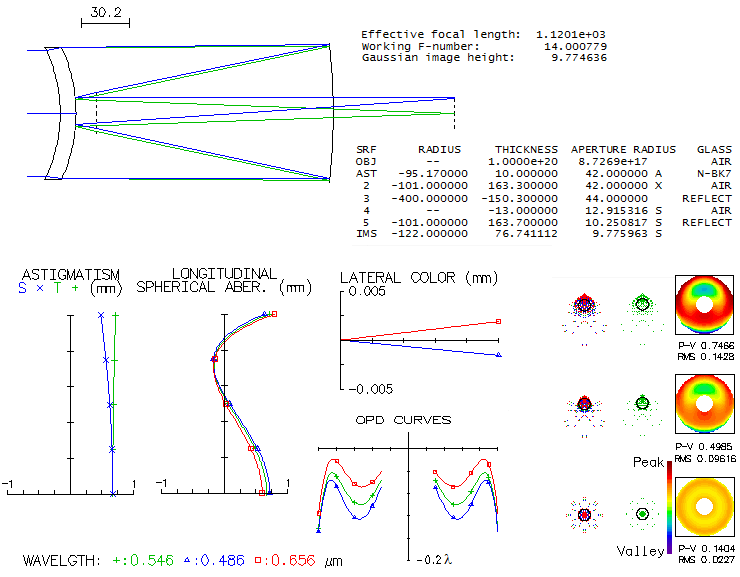But, as mentioned before, the Mangin MCT can have its meniscus radii significantly more relaxed, reducing the higher-order spherical residual, with the chromatic defocus induced compensated by a change in the front, refractive radius of Mangin mirror. Below is an example of the initial Mangin MCT with significantly more relaxed meniscus radii.

The system becomes more compact, faster (f/9.8), with the correction error in the optimized wavelength nearly cut in half, with even less astigmatism and 22% lower lateral color error (still more than double the error in the standard MCT), but the price to pay is the larger central obstruction - nearly 32mm (40%). Field curvature is more relaxed at -144mm radius, vs. -99mm in the standard MCT (-122mm in the prescription is an oversight). Overall, while using Mangin primary is a viable option, aspherizing the primary achieves similar benefits in making a system more compact and faster in a generally simpler way, without negatively affecting lateral color error. It is also less expensive vs. having another piece of high-quality optical glass and an extra spherical surface to make. That is why it is the preffered choice for manufacturers.

VESELKOV-MAKSUTOV TELESCOPE

In general, a compact MCT telescope has three residual aberrations, that can be significant: astigmatism, coma and field curvature. Astigmatism is generally low, coma varies with the system, i.e. contributions of the meniscus and secondary vs. opposite in sign primary contribution, and field curvature is inconsequential visually, but not in imaging. While coma-free MCT systems are possible, they require small secondary. The idea of MCT modification by Veselkov (RU 2,449,329 Veselkov S.A. 2012) was to make possible coma-free compact MCT with nearly flat field for faster systems as well. To accomplish this, it was needed to aspherize secondary, which removes coma, and set the radii of primary and secondary mirror equal, in order to make Petzval curvature zero. Remaining mild field curvature is a result of system astigmatism. Minimum secondary diameter is just over 92mm, but the central obstruction would have to be at least 100mm, or 50% linearly.

Top system is a Veselkov-type MCT. The original system described in the patent application is a 200mm f/8, but the main characteristics remain nearly unchanged with this, somewhat faster system: mild field curvature caused by the system astigmatism, and coma-free field (box below the system drawing shows 0.5° spots and diffraction images for the same system with spherical secondary). The secondary conic is interchangeable with the meniscus distance: the closer meniscus, the higher conic. The requirement of equl mirrors' curvature radii inevitably sets the secondary large, in order to have accessible final image. At 0.5° off axis, there is berely detectable deformation of the central maxima due to field curvature, but the elongation due to lateral color error (even sensitivity) is readily noticeable. Field can't be made truly flat, since nearly of the astigmatism comes from the primary. Compensating for astigmatism by non-zero Petzval would require significantly weaker, i.e. larger secondary. Considering that 1-degree field in diameter is well corrected overall, it wouldn't be justified.

For larger fields, both field curvature and lateral color can be corrected with a single meniscus field corrector (middle). Required conic on the secondary diminishes with the secondary size; with the minimum size below 60mm (diameter), a coma-free flat-field all-spherical system is possible (bottom). Note that the field meniscus still has identical parameters, with the blue/violet slightly undercorrected laterally, but it does not have noticeable effect on the diffraction image.

◄ 10.2.3.2. Maksutov-Newtonian ▐ 10.2.3.4. Maksutov-Cassegrain aberrations ►

Home | Comments