|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
13.3. Eye aberrations
▐
13.4.2. 2nd order defocus and astigmatism, off-axis
► 13.4. MONOCHROMATIC EYE ABERRATIONS
PAGE HIGHLIGHTS
The list of most significant monochromatic eye aberrations
includes
defocus, astigmatism, coma,
spherical aberration, and trefoil, as
well as optical roughness, caused by
local surface deformations and
lack of media homogeneity. Even a good average eye generates enough of a
wavefront error to require pupil diameter smaller than 2mm for near
diffraction-limited level (~λ/14 RMS wavefront error for 0.55μ
wavelength). Due to the typically highly asymmetrical, irregular wavefront shapes produced by human eye, especially at larger pupil sizes, the method of choice for assessing eye aberrations are Zernike circle polynomials. However, Zernike scheme commonly used in ophthalmology - the ANSI standard Zernike expansion - is different from those used in assessing telescope aberrations. It is graphically presented as a pyramid resulting from Zernike term expansion as a function of radial order n and angular frequency m, with the latter being numerically positive for cosine function of θ, and negative for the sine function (FIG. 225; the relation between the sign of m and the function is illustrated on FIG. 30, 4). The terms are ordered and enumerated according to the specifically defined ordering number j.
Piston and tilt (distortion) terms usually are omitted from consideration, the former due to being zero for single-pupil imaging, and the latter being an aberration affecting point image location, not its quality. The common division of the expansion terms is on the lower, or 2nd order aberrations (defocus and astigmatism), and higher-order aberrations. The latter include unlimited number of terms, but usually limit to orders 3 to 5, or 3 to 6, since yet higher orders are generally negligible. Following the above division of the Zernike expansion adopted in ophthalmology, monochromatic eye aberrations are addressed as: (1) lower-order aberrations, with the Zernike radial order n<3, and (2) higher-order aberrations, with n≥3. This division is particularly appropriate for the concept of eye aberrations, because the lower-order aberrations - and particularly the 2nd order aberrations, defocus and primary astigmatism - are the most significant contributors to the overall magnitude of eye aberrations (remaining lower-order forms, piston and tilt, or distortion, are usually ignored, with the former being not an aberration with a single imaging pupil, and the latter being not a point-image quality aberration). Monochromatic aberrations in an optical system are commonly separated into axial, occurring in the field center, and off-axis, occurring in the outer field as a result of the obliqueness of incident light pencils. Correction of the former is the primary goal, since objects are generally observed in the central field. Unlike typical telescope systems, which - if properly made and aligned - consist of rotationally symmetrical surfaces centered around optical axis, the eye operates in inherently misaligned mode, with surfaces lacking rotational symmetry to a significant degree. As a result, typical off-axis aberrations in a telescope (e.g. coma and astigmatism), are commonly present in the fovea, as well as in the outer retina (the difference being that the latter originate mainly from the obliquity of incident light pencils, reaching significantly larger magnitude at large incident angles) . Thus terms axial and off-axis, when associated with eye aberrations, do not imply specific group of aberrations, as with telescope systems, rather any aberrations appearing in the central retina, as a result of eye imperfections. Axial (also central, or foveal) eye aberrations are the primary limitation to its proper functioning both, in daily life and as a part of optical train involving use of a telescope. Off-axis (also oblique, or abaxial) eye aberrations are comparatively unimportant, but will be also addressed, since they can affect quality of extended object images, or extended fields projected onto the retina.
Generally, the magnitude of aberration contribution
decreases with increasing Zernike radial order. Second order aberrations
account for roughly 90% of total aberration of the average eye. The most
significant higher-order terms are 3rd order coma and trefoil, and 4th
order spherical aberration, as summed up in the table
below (as mentioned before, zero-order piston is not an aberration for
image formed by a single aperture, and 1st order tilt/distortion is not
a point-image quality aberration; for that reason, they are usually
omitted from evaluating eye aberrations). RADIAL
ABERRATION ZERNIKE TERM ZERNIKE COEFFICIENT ZERNIKE Double-index Single-index Double-index Single-index 2ND Oblique primary
astigmatism
Z Z3 z2,-2 z3 ρ2sin2θ Defocus
Z Z4 z2,0 z4
2ρ2-1 Vertical primary
astigmatism
Z Z5 z2,2 z5
ρ2cos2θ 3RD Vertical trefoil
Z Z6 z3,-3 z6 ρ3sin3θ Vertical primary
coma
Z Z7 z3,-1 z7 (3ρ3-2ρ)sinθ Horizontal primary
coma
Z Z8 z3,1 z8
(3ρ3-2ρ)cosθ Oblique trefoil
Z Z9 z3,3 z9
ρ3cos3θ 4TH Primary spherical
aberration
Z Z12 z4,0 z12
6ρ4-6ρ2+1 Following
the main division of
monochromatic eye aberrations on lower and higher orders, according to
the ANSI Zernike terms expansion, the text continues with more detailed
description of 2nd order eye aberrations, on axis (foveal) as well as
off-axis. Next page addresses higher-order eye aberrations. 13.4.1. 2ND ORDER ABERRATIONS:
AXIAL DEFOCUS AND ASTIGMATISM As already mentioned,
defocus and 2nd order (primary) astigmatism account for roughly 90% of
the total monochromatic aberration of the average eye. Among the two,
defocus is clearly dominant, being up to several times larger in
magnitude. Axial (foveal) defocus and
astigmatism are addressed first, followed with a description of off-axis
extent of these two aberration forms. Axial defocus
In ophthalmology, defocus is
second-order aberration,
denoted with the Zernike term Z Axial eye defocus is caused primarily by the mismatch between optical and/or accommodative power of the eye and the size of vitreous body; other contributing factors can be weakened muscles surrounding eye lens, and/or lack of elasticity of the lens itself. The more the separation between cornea and retina deviates from 23-24mm, the more likely significant axial defocus error; in general, larger eye tends to suffer from myopia (short focus for distant objects, improving with reducing object distance), and smaller eye from hyperopia (long focus for distant objects, worsening with the reduction in object distance). Overgrowth of the vitreous body - either as a whole, or as an elongation along visual axis, or as an outward deviation in the concavity of the rear retinal wall - is much more common than undergrowth, hence myopia is also more frequent than hyperopia. Farther off-center, retinal shape (contour) - which is generally prolate ellipsoid, but of varying vertex radius, conic and local deviations - is also a factor that can be significant in determining the magnitude of defocus error, and so are the Petzval and astigmatic field curvature. Together with optical power of the eye, these are the factors determining the magnitude of off-axis defocus error, which is addressed in the subsection on off-axis eye aberrations.
Following table is a short summary of defocus-related
terms and relations (z4 value obtained from the P-V wavefront error is in wavelengths,
and to obtain its value in microns needs to be multiplied with the wavelength expressed in microns).
Average accommodation power of the eye decreases with age, from 10-15 diopters at age 20, to 1-2 diopters at age 60 (FIG.
221
bottom left).
Accommodation power in diopters can be expressed simply as 1/S, with S
being the eye-to-object separation in diopters (i.e. in units of 1
meter); hence accommodation power of 10 diopters implies ability of eye
lens to
refocus from zero (object at infinity) to 0.1m, and 1 diopter
accommodation power implies ability to refocus from infinity to objects 1m away.
The smallest distance at which eye can sharply focus is
referred to as the least distance of distinct
vision or, more simply, near-focus distance.
Diopter (or
dioptre, abbreviated by D), expressed as D=1/f, in which f represents the lens power (focal length)
in meters, is used as a
measure of longitudinal defocus. Since the effective focal length of the eye
(the f.l. that the eye would have with air as imaging medium) is fE~17mm,
or ~0.017m, its diopter is ~59. The larger diopter, the stronger optical power,
i.e. the shorter focal length. The
difference between the optical powers of rays from the central and outer zones of
eye pupil
indicates the amount of defocus. A 2D defocus caused by a different
optical power of the outer zone of the eye lens means that the outer
zone diopter is 61. In effect,
it is by ~1/30 of the proper focal length shorter, as if formed by rays
falling onto the eye lens being slightly converging. Negative diopter
indicates that the outer zone focuses longer. Thus -2D defocus indicates
57D power for the outer zone of the eye lens, or focal length by 1/30 of
the central rays' focal length longer, as if coming - approximately -
from a point not at infinity, but located at 30 eye lens' focal lengths - or 2 diopters - in front of the eye.
Formaly, diopter prescription with eye defocus indicates the power of lens needed to
correct the aberration. So if eye defocus is, for instance, 3 diopters,
making its focal length 62 diopters, it will be corrected by putting a -3D
lens (negative, with focal length of -1/3 meter) in front of the
aberrated eye. This
is due to the
combined focal length being approximated with a thin lens equation, as
1/fC=(1/fE)
+(1/fG),
which for focal lengths in diopters becomes DC=DE+DE,
with subscripts
Defocus expressed in diopters, D*, can be converted into longitudinal defocus L,
as L~D*fE/60,
and from it into P-V wavefront error W=L/8F2
which, with the focal ratio F~17/P, where P is the eye pupil
diameter, can be written as W=LP2/2300.
Substituting D*fE/60 for L, and taking fE~17mm,
in terms of defocus error in diopters D* it becomes W=D*P2/8100.
So, for instance, one diopter of defocus results in 0.23 wave P-V wavefront error at 1mm pupil, and 5.7 waves
at 5mm pupil (for 550nm wavelength). The corresponding RMS wavefront error is smaller by a factor 1/√12,
and equals absolute value of the Zernike expansion coefficient. Denoting RMS error with
ω, it can be written as ω=|D|P2/28,000.
Solving for P and ω=0.000041mm (diffraction limited RMS error for
0.00055mm wavelength) determines the limit for diffraction limited
defocus error in diopters as D*~1.15/P2.
That gives 0.29 diopters defocus limit at 2mm pupil diameter, and 0.13
diopters at 3mm pupil diameter. It is safe to say that relatively few individuals have natural eyesight with such a low level of defocus error. Looking at a few recent studies, inherent eye defocus errors are quite common, and often quite large. For instance, among 109 "normal" participants aged 21 to 65 years (41y average), defocus, or spherical refractive error was between +6D and -12D (-3D mean, +/-3D standard deviation). The average eye here (Porter et al. 2000)is far from diffraction limited even at 1mm pupil diameter. Another study on 100 students of Indiana University School of Optometry, aged 22-35y (26.1y average), had nearly identical overall defocus error, +5.5D to -10D range, with -3.1D mean +/-3D SD (Indiana Aberration Study, Thibos et al. 2002). These numbers indicate that eye defocus error does not increase significantly with age. In the Indiana Aberration Study, only about 20% of participants had defocus error less than 1D. Majority had myopia (short sight, numerically negative defocus error), which is representative of the population in general. Yet another group of students, this time from Murcia University, Spain (59 students, 20-30y old, 24y average) had significantly lower defocus error at +1.3D mean +/-1.7D SD (Castejan-Mochan et al. 2002). These numbers, on the other hand, indicate that there may still be substantial random variability in groups of this size. Between about 3D average defocus error in the first two, and 1.3D in the third study, a broad population average may be at 2-2.5D level. With the corresponding RMS wavefront error ω=DP2/16√3 in microns, the uncorrected average eye would be diffraction limited defocus-wise (for 0.55μ wavelength, thus ω=0.55/√180) roughly at a pupil diameter P of 0.7mm. However, regardless of the magnitude of defocus error in the eye, it does not affect the telescope observer: s/he corrects for it by defocusing the eyepiece by an offsetting amount. It is another focusing-related eye function that can have the effect on perceived image quality in a telescope - specifically, quality of the outer field. It is the eye accommodation power. The image field produced by telescope objective is usually curved, not seldom quite strongly. Depending on the the sign of curvature, it causes outer field image points to be progressively closer, or farther away from the eyepiece. This, in turn, causes these light pencils to exit the eyepiece slightly diverging (when closer) or converging, i.e. appearing as coming from a finite distance. In order to bring these pencils into focus, eye has to accommodate, primarily by changing the shape of eye lens. The eyepiece itself can produce strong image curvature, which can make curvature of the final best image surface either stronger or weaker than that of the objective's image. Neglecting effect of the eyepiece - whose specific image curvature is commonly unknown - the power of accommodation required due to the curvature of image formed by the objective can approximated using basic paraxial relation (Eq. 1.4). Substituting f+(h2/2R) for object distance, with f being the eyepiece focal length, h being the point height in image space and R the radius of image curvature, gives the apparent point distance p as: p=2R(f/h)2+f. With f and h in mm, the corresponding accommodation power in diopters is 1000/p. For, say, image curvature radius R=100mm, eyepiece f.l. f=10mm and point height h=5mm (which is at a field edge of the standard 10mm 50° AFOV eyepiece), p=810mm and needed power of accommodation is 1.2 diopters. This level of accommodation is achievable for most people, and quite easy for younger individuals. However, with significantly wider field, or significantly stronger field curvature, or with the eyepiece significantly adding to the final image curvature, older individuals may not be able to see the outer field clearly without adjusting the focuser. The specific form of image curvature, i.e. whether it is concave or convex toward the eye, is an additional factor that influences how demanding is accommodation. It is harder for the eye to focus a converging beam - such as one coming from off-axis point farther away than the center (i.e. from outer portion of image surface convex toward the eye - since it is not a natural geometry, requiring eye lens to weaken its surface curvatures beyond those needed for focusing near-collimated beam. The next largest axial aberration of the average eye is primary astigmatism. It is mainly the combination of eye's defocus and astigmatism that is mainly responsible for often grotesquely deformed, stretched out diffraction patterns produced by the eye at larger pupil sizes. As mentioned, eye defocus error is inconsequential for visual observing with a telescope, which acts as a corrective aid. Unfortunately, this automatic correction does not extend to eye astigmatism.
Axial astigmatism
Like defocus, primary astigmatism in ophthalmology is second-order aberration,
denoted with the Zernike term Z
Astigmatism
in human eye can be axial, which most often originates at the cornea, prone to
relatively weak cylindrical deformations, or regular off-axis
astigmatism. The extent of the former is determined by the severity of
corneal deformation, while the latter, in general, becomes progressively larger with
the increase in off-axis
angle (i.e. with the increase in retinal eccentricity).
2ND ORDER
(PRIMARY) ASTIGMATISM
Zernike z3
and
z5
to diopters conversion combined z3
and z5
terms coefficients order j-number single-index D=-8z3√6/P2
= -J45
J=J0+J45 =(J02+J452)1/2 P-V=z3√24
Z
z2,-2 2 3
Z3
/ z3
Astigmatism Zernike coefficients z2,-2
and
z2,2
converted to diopters (i.e. astigmatism wavefront to longitudinal error)
for the purpose of ophthalmic glasses prescription, are commonly denoted as J45
and J0
or J180,
respectively (not to confuse with the j-number). The former is termed
oblique astigmatism, and the latter vertical/horizontal
astigmatism (in ophthalmic terminology, the latter is called
with-the-rule and against-the-rule astigmatism, with the
former - prevalent in children - being caused by the vertical wavefront
radius stronger than horizontal, and the latter - prevalent in adults -
the other way around).
Note that oblique astigmatism related to the Zernike term is not
to be confused with the regular off-axis astigmatism on the retina,
frequently also referred to as oblique astigmatism. The former is
so called asymmetrical (or antisymmetrical) term used to describe
astigmatic wavefront with the two main astigmatic meridians at an angle
different than 90°. In other words, when the
two astigmatic corneal axes are not perpendicular, the oblique
J45
mode is used to better approximate the shape of resulting wavefront deviation.
When both, J0
and
J45
terms are present, their combined value is given by the square
root of the two values squared: J=(J02+J452)0.5.
The resulting deviation from 90°-angle between two meridians - called
axis - is given by 0.5[tan-1(J45/J0)]
or, for that matter, by 0.5[tan-1(z3/z5)].
Axial astigmatism in the average eye is only a fraction of its axial defocus
error. Turning to the same three studies cited with defocus, the astigmatism-to-defocus ratio
ranges from about 1:10 (Indiana Aberration Study, as the mean
longitudinal error in diopters) and 1:7 (Porter et al. as the absolute RMS
wavefront error) to 1:3.6 (Castejan-Mochan et al.), the last one as the mean Zernike expansion
coefficient. None of the studies
are directly comparable, the first having the aberration expressed as
longitudinal (in diopters), as opposed to RMS wavefront in the second,
and Zernike coefficients in the third study (Zernike coefficients
numerically equal the RMS wavefront error but, unlike it, can have
negative value as well, hence different - generally smaller - mean
value).
Longitudinal astigmatism error in diopters J=0.3D from the Indiana study
can be converted back to the corresponding combined mean Zernike
expansion coefficient for astigmatism as zAc=JP2/16√6,
(assuming J~J0,
with the latter usually amounting to most of J value)
where P is, as before, eye pupil diameter. For defocus, conversion relation
is z2,0=D*P2/16√3,
hence defocus coefficient vs. that for astigmatism is larger by a factor of √2
for given longitudinal error (this merely reflects the difference in the P-V/RMS error
ratio between the two aberrations; since the P-V error expression for given longitudinal error
is identical for defocus and primary astigmatism, so is the P-V wavefront error for given defocus in diopters,
as specified for defocus error above). Thus, in terms of Zernike coefficients,
the astigmatism-to-defocus error ratio in the Indiana study is 1:14, or
nearly four times smaller than 1:3.6 (also in terms of Zernike
coefficients) in Castejan-Mochan et al.
The ratio in the third study, Porter et al., is not directly comparable these two
studies, since mean errors were calculated from the absolute values of Zernike coefficients,
i.e. from the RMS values. Since
that excludes partial offset between positive and negative coefficient
values, this average value reflects the actual average of error
magnitude, and will give a
higher mean value. It can't be specified by how much without knowing
the raw data. Absolute average will be greater for both, defocus and
astigmatism, but less so for defocus, which is mainly myopic, with
negative coefficient values. Values more comparable to a mean of absolute values are
usually those of the standard deviations from mean for both, positive
and negative values. Taking standard deviation from the Indiana and Spanish study
instead of the means, gives astigmatism-to-defocus ratio for the two of 1:11 and 1:2.3,
respectively, which should be at least roughly in the same form as the 1:7
ratio from Porter et al.
These three ratio values are too widely separated to indicate, at least approximately,
astigmatism-to-defocus ratio in the general population. The values
clearly indicate that some
study populations were biased toward atypical averages either for
defocus or astigmatism, or both. Averaged astigmatism-to-defocus ratio
for broad population is very likely between 1:10 and 1:3, still too
broad to be useful. Including ratio values for sample
populations from two other studies gives somewhat better idea of the
average ratio value: 5.1 (Cheng et al. 2004, 74 subjects aged 21-40
years, -2.50D+/-2.25D mean defocus error and
-0.70D+/-0.54D primary astigmatism, the latter
subject to √0.5
correction factor for conversion to wavefront errors), and 1:6.6 and
1:2.4 for ~23 and ~60 years of age, respectively (McLellan et al. 2001,
38 subjects aged 23-65 years, as a ratio of mean astigmatism to mean
spherical equivalent refractive error), place the simple ratio average
for these five studies between
1:4 and 1:5. However, the last study indicate that the ratio value
varies significantly depends with age.
In part, these ratio discrepancies are due to the variations in the level of astigmatism of
sample populations: average axial astigmatism is over 50% greater in Castejan-Mochan
et al. vs. Porter and al., with the latter having it about 1/3 higher
than Thibos et al. Thus nearly half of the discrepancy in the
astigmatism-to-defocus ratio comes from the difference in the level of
astigmatism from one study population to another.
Sample-to-sample variations in the average defocus error are even more
significant. For instance, range of defocus error was
significantly wider for participants in Porter et al. and Indiana study
(+6D to -12D and +5.5D to -10D, respectively), than in Cheng et al.
(+1.25 to -8.25D) and McLellan et al. (+0.5D to -6D, with a single
extreme positive subject with +4.6D excluded from regression analysis;
plot based on McLellan et al. is shown at left, with raw defocus values
substituted by "spherical equivalent refractive error", somewhat
modified by combining it with spherical aberration present, but
gravitating toward the raw values).
Obviously, this degree of random variations in the average axial defocus
and astigmatism in study populations will inevitably result in a wide
range of their ratio value.
It shows that these sample sizes, despite being relatively large by the
standards applicable to eye aberration research, are still to small to be reliable
indicator of the average magnitude of these two major axial eye aberrations in
the general population. Considering age dependence for the two
aberrations implied by McLellan et al., the average
population astigmatism-to-defocus ratio, very
approximately, could range from 1:7 in the early twenties to about 1:3 in late fifties.
As the above graph indicates, most of the increase in the ratio value is
due to the increase in averaged astigmatism, which more than doubles
from age 20 to age 60. Decrease in averaged defocus with age is
comparatively small.
Since defocus and axial astigmatism make about 90% of the total axial
aberration of the average eye, astigmatism alone accounts for about 15-30%
of it, less in younger population, and more in the
older one. Again - and as the above graph shows - individual deviations
from the overall average are wide and unpredictable.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
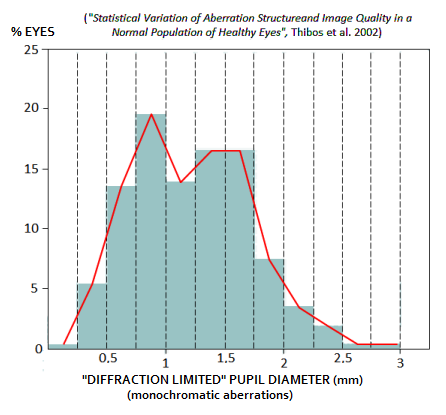 Graph at left shows statistical distribution of the "diffraction limited" pupil diameter according to a study. It indicates that most people fall between 0.5mm and 1.7mm, with the rough average at about 1.2mm. The
combined error increases and decreases progressively with the pupil diameter.
Graph at left shows statistical distribution of the "diffraction limited" pupil diameter according to a study. It indicates that most people fall between 0.5mm and 1.7mm, with the rough average at about 1.2mm. The
combined error increases and decreases progressively with the pupil diameter.