|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
6.6.1. MTF - aberration compounding, CCD, limitations
▐
7. OBSTRUCTION EFFECTS
►
6.7. COHERENT TRANSFER FUNCTION, FOURIER TRANSFORM
As
mentioned before, optical transfer function (OTF) is defined for
incoherent light, hence so are its elements, including MTF. While the light
entering telescopes is generally incoherent, it can not be considered
fully incoherent, and the degree of its incoherence varies (spatial
coherence, according to Van Cittert-Zernike
Theorem, can vary with the apparent object size). As mentioned in
2.2. Telescope resolution, there
is no difference in the relative intensity distribution between
incoherent and coherent light in imaging a point source, as long as it
is near-monochromatic in incoherent light, but there are significant
differences in imaging multiple close point sources and extended
objects. In that context, it
may be interesting to see what effect on contrast transfer would have
change of illumination from incoherent to coherent.
In comparing transfer function for coherent and incoherent light, the
difficulty arises from different natures of the two. While image of an
object in incoherent light forms by superimposing point intensity
distribution (system PSF) over Gaussian image of the object, with the
intensities at each point directly adding up, with coherent light the
image forms by superimposing point image amplitude distribution
(coherent spread function, CSF) on every point of Gaussian image, with complex amplitudes
at each point adding up to the final point complex amplitude (in that
context, we are talking about amplitude image). Squaring this
complex amplitude image produces intensity distribution over object's
image.
In other words, image in incoherent light is the convolution of the
Gaussian (intensity) image and the system PSF, while image in coherent
light is the convolution of the Gaussian (amplitude) image and the
system CSF. While in the former intensity forms as a superposition of
individual waves, which randomly varying phase relationship, in the
latter individual waves have constant phase relationship, and interfere
building up complex amplitude, the square of which is
intensity (Inset
G).
Due to its different mechanism of image formation, the standard
(incoherent) OTF formalism cannot be applied to coherent light The
standard transfer function for coherent light - coherent transfer
function (here abbreviated by ATF -
for amplitude transfer function - to make it different from the
Contrast Transfer Function in the
abbreviation) - describes
the transfer of amplitude, not intensity. More importantly, coherent
light diffracts differently with different object intensity profiles,
making ATF much more limited to the special case of a sinusoidal object
amplitude distribution, than OTF. For instance, if sinusoidal pattern is
replaced by square wave pattern (sharply outlined black and white bars),
coherent light diffracts differently and is likely to produce blurred
edges (Gibbs effect, or ringing edges).
Lastly, ATF neglects phase disturbances that arise from uneven
object surface, producing random interference pattern of bright and dark
spots - speckle structure - which can significantly worsen image
definition.
As such, ATF is much less useful as a general indicator of image
quality than the OTF. For the same sinusoidal OTF-like pattern - which is this time the
amplitude, not intensity - ATF gives a very different transfer profile.
Optical context from which ATF is derived is illustrated below. Since
its key component is Fourier transform of the pupil function, it is
followed
with a brief outline of the concept of Fourier transforms.
For aberration-free aperture, there is no drop in the amplitude transfer for the entire range of
frequencies up to the cutoff frequency. However, the cutoff frequency is
1/2λF, only half the resolution power in
incoherent light.
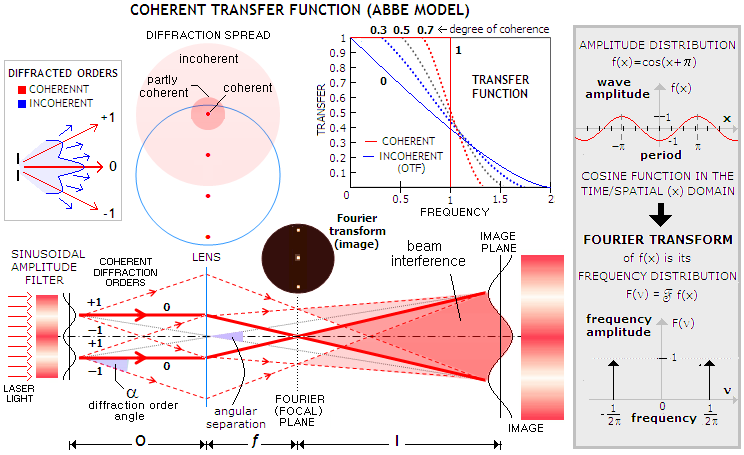
This
doesn't seem logical, since it appears that diffraction vanishes up to
the cutoff frequency, only to entirely block amplitude transfer in an
instant, at the twice lower frequency. In fact, there is a lot of
diffracting taking place, as illustrated at left, but in this particular case
diffraction is sort of "undoing" itself - at list up to a
point. At
the sinusoidal amplitude filter, coherent light diffracts in a peculiar
way, with only two diffraction orders splitting some energy away from
the zero order. The angle of diffraction is given by sinα=λ/w,
with
λ
being the wavelength of light and
w
the line width. As long as the two side diffraction orders pass through the
pupil, they will come together forming beam interference with each other
and the zero order beam at
the image
plane, forming sinusoidal intensity distribution, modified vs. that of
the object only
by the system magnification. As the grating frequency increases, the
diffraction orders spread wider; they just miss the pupil at the
frequency 1/2λF, and the transfer function
abruptly falls to zero.
For the resolved image to form it is sufficient that only a single
diffraction order passes through, and combines with the zero-order at
the image plane. This means that the cutoff frequency can be up to twice
as high - equal to that for incoherent light (1/λF) - if amplitude
filter is
tilted with respect to the lens.
Unlike coherent, diffracted incoherent light fills the entire pupil, so that a
portion of it still passes through the pupil as the diffraction spread
widens (top left), up to a frequency twice higher than for coherent
light. However, as the signal passing through becomes more and more
incomplete, its contrast transfer is steadily declining toward the
high frequency cutoff, which is double that for the ATF, since less and less of information from the
object reaches the image. For light that is neither coherent or
incoherent - taking various degrees of partly coherent, or partly
incoherent - the transfer function falls somewhere in between (top right).
It should be noted that partly coherent/incoherent transfer functions
are, similarly to ATF for coherent light - and unlike OTF - quite
limited as indicators of image quality. and cannot be considered valid
for a wide range of object/image forms.
In the above illustration, the grating is located at the system aperture, and it is where the
diffraction is taking place - not at the lens.
Note that the size of the grating is greatly
exaggerated for clarity; close to the ATF transfer limit, the two
adjoining maximas would be much closer together, and the two triangles
formed by their respective +1/-1 diffraction orders would be nearly
coinciding, with their points of origin located close to the central
axis. Hence the geometry determining cutoff frequency
wc
comes from sinα=λ/wc=d/c,
where d
is the aperture radius and c
is the triangle hypotenuses. That yields wc=cλ/d
and, since the linear value of wc
changes with grating distance, with its angular value remaining
unchanged, we can chose a convenient value for
c
to express wc.
Such value is c=f
(f
being the lens focal length), for which the infinitely large image forms
at infinity, with wc=2λF
and its angular value - as the angle whose base is wc
and the tip is center of the objective (in the thin lens concept) is
given by wc/f
i.e. 2λ/D radians - twice lower cutoff
frequency than for incoherent light.
This is also the setup for which the pattern formed in the focal
(Fourier) plane is exactly the Fourier transform of the sinusoidal
pattern. The lens is often referred to as Fourier transform lens,
but it is diffraction at the amplitude filter (grating) that does the
transform; the lens merely brings the transform pattern from infinity (or,
approximately, Fraunhofer domain) to its focal plane. The 3-point
intensity pattern illustrated in the focal plane of the lens is
proportional to the function representing the frequency distribution of
the cosine function shown in the shaded inset at right. Since the cosine
function consists of a single frequency, its frequency amplitude spectrum
(i.e. Fourier transform) is graphically represented as a single delta
function (vertical bar) at the unit frequency - called fundamental
frequency, as the reciprocal of the period of the cosine function - and unit (in relative terms) frequency
amplitude. Expanding frequency spectrum into negative domain is not
necessary to define the Fourier transform, but it is a common practice,
since it simplifies related expressions and calculation.
In general, frequency amplitude distribution F(ν) - commonly
referred to as frequency spectrum - of the fundamental frequency
and harmonics that reproduce (or, in the opposite direction, decompose) a function f(x)
in the time/spatial domain (i.e. with the variable changing as a
function of time, and/or space) is its Fourier transform, or F(ν)= Ff(x),
with f(x) being the inverse Fourier
transform of F(ν), or f(x)=F-1F(ν).
The significance of the Fourier transform - i.e. frequency spectrum - of
the generalized wave function is that it defines the relationship
between incident and diffracted field amplitude. More specifically, the
amplitude of the diffracted field is proportional to the amplitude
distribution of its frequency spectrum. In other words, diffracted field
is (at infinity) proportional to the Fourier transform of the incident
field. As such, Fourier transform concept is universally present in
imaging, and deserves a more detailed overview.
FOURIER TRANSFORMS
The basis of the Fourier transform concept, as postulated by the French
physicist Joseph Fourier, is that any function form - in our case
electromagnetic signal - can be produced by summing up sinusoidal waves
of different frequencies and amplitudes; or vice versa, any function
form can be decomposed into such an infinite series of harmonics. Such a series is called
Fourier series. Being for
an even, i.e. mirror-symmetrical about Y-axis function, this square wave
series only contains cosine terms. If periodic function has the same
pattern above and below X-axis (which would be the case for square wave
function where one edge coincides with Y-axis) it is called odd,
and is represented by Fourier series consisting of sine terms alone,
while all cosine terms are zero. If a function is not neither even, nor
odd, its Fourier series consists of both, cosine and sine terms, both as
an infinite series decreasing in amplitude while increasing in
frequency. General form of the Fourier series representing f(x) can be
written as:
f(x)=C+∑Acos(m νx)+∑Bsin(mνx)
where C is the constant that positions
function vertically in the coordinate system, A is the amplitude
coefficient varying with the cosine terms, B is the amplitude
coefficient varying with the sine terms, m is the integer (m=0, 1,
2, 3,...) in either of the two series of terms, and
ν is the fundamental
frequency, which is the basis for synthesis of the series' harmonics
(sinusoids of higher frequencies) by multiplying it with m.
Formally, Fourier series consists of an infinite number of terms - base
(fundamental) frequency term and higher frequency terms, called
harmonics - but in
practice it is limited to the number needed to reproduce a function with
needed accuracy. The more terms in the series, the more closely reproduced the function.
Such a series can reproduce any function, periodic or non-periodic.
Shown below is a Fourier series for periodic square wave (which can
represent amplitude distribution produced by
the Ronchi grid in coherent light).
Both, unit frequency and period are those of the square wave, f(x). The period is 4, its frequency 1/4
(meaning that 1/4 of the full period is contained in the scale unit),
and its angular frequency is π/2
radians, meaning that there is 1/4 of the full phase of 2π
radians per scale unit.
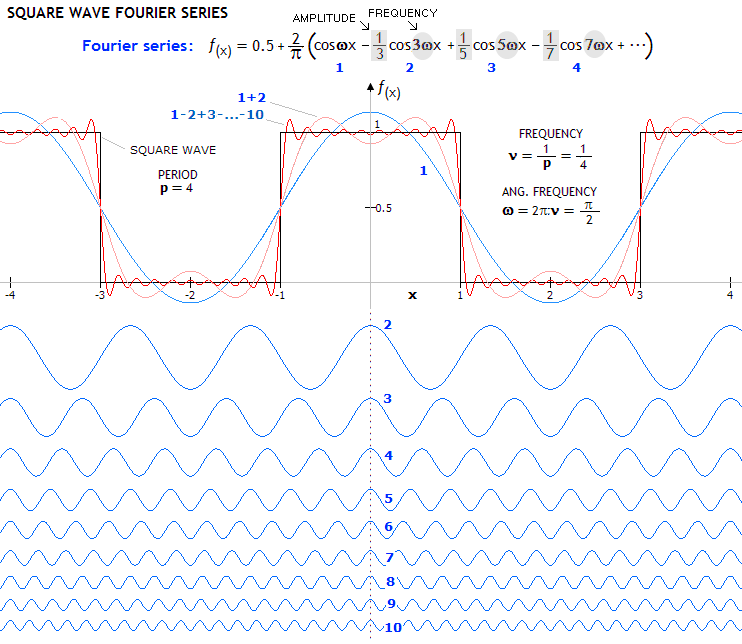
Unlike the sine pattern, square wave pattern will not be reproduced as
the original pattern in coherent light, even if it is of low frequency
and with many orders captured. One form of distortion - ringing edge -
is readily visible, and does not significantly subside in the magnitude
with the increase in the number of terms (i.e. orders caught by the
lens), only becomes more dense. On the other hand, incoherent light with
its randomly fluctuating diffraction orders will much more evenly fill the edges with energy, forming
better defined image. As the number of terms increases (since the
function is even, all sine terms are zero), the sum of terms more closely approaches square wave
form.
The amplitude coefficients for each frequency
are the basis for the frequency spectrum associated with square wave
function, i.e. they describe its
Fourier transform. Unlike sinusoidal
wave, having a single frequency amplitude in the positive domain (i.e.
forming a single bright off-center spot in the Fourier plane), frequency
spectrum for square wave distribution is enveloped within sinc function,
with an infinite number of steadily decaying discrete frequencies, as
this series indicates (in other words, it will form an infinite number
of off-center bright points lined up in the Fourier plane, steadily
diminishing in intensity the farther off they are). Each of those points
signifies one diffraction order originating at the grid and spreading
wide. The more orders are being caught by the lens bringing the
Fourier
transform of the square wave field to the focal plane, the better
defined the image formed in the image plane (as illustrated in the Abbe
model above).
Graph below shows the square wave frequency spectrum in its sinc
function envelope. The unit frequency is for a sinusoid with the same
period as the square wave, with the odd numbers on the horizontal scale
corresponding to the numbers for the Fourier series terms given above (1
on the scale for 1 in the series, 3 on the scale to 2 in the series, and
so on, since the frequencies are increasing with an odd multiplier).
The amplitude for each harmonics is (2/ π)A,
with A being the numerical constant for the term (for instance,
A=1 for the first term, and its relative amplitude in the frequency
spectrum is 2/π).
As mentioned, all sine terms of the Fourier series for even function,
hence for the transform too - falling on even frequency integers of the
frequency spectrum - are zero. This is obvious here, since the basic
frequency is π/2
(90 degrees), which gives zero when multiplied with any integer.

As periodic wave transforms into pulse wave, with
pulse separation greater than their length, relative frequency of the
harmonics diminishes, with the corresponding frequency spectrum becoming
more dense (top left, for the pulse wave with the period double that of
the periodic square wave). When pulse separation reaches infinity, the
function becomes a single square pulse, and its frequency spectrum -
i.e. Fourier transform - becomes continuous sinc function (top right).
Continuity of the frequency spectrum imply that the amplitude
distribution in the Fourier plane is not in the form of discrete points,
rather a continuous amplitude/intensity distribution, with each point of
light in it signifying specific, corresponding to it harmonic frequency.
It should be noted that, formally, "Fourier transform" generally refers
to the continuous spectrum function, such as a single pulse, as opposed to "discrete Fourier
transform", referring to the discrete spectrum of a periodic
function.
Fourier
transform of a single square pulse is particularly important, because it
(square pulse)
is a function describing aberration-free exit pupil of an optical system
with even transmission over the pupil area.
Consequently, we recognize in its Fourier
transform the familiar shape of the coherent (point) spread function
(CSF, which is, in effect, point amplitude-image), whose squared modulus (magnitude) is the
PSF.
In turn, pupil function is the basis for calculating ATF and OTF. While
the ATF integral shows that it is merely a scaled pupil function, with
amplitude transfer equal to 1 for frequencies lower than 1/2λF and equal
to 0 for higher frequencies, OTF is equal to the autocorrelation of its
pupil function. With pupil function defined by the amplitude (electric
field) and phase in the plane of exit pupil, the aberration free pupil with even
transmission is a square wave function in 2-D, and a cylinder in 3-D.
With pupil amplitude normalized to 1, OTF is proportional to the area of
overlap of the pupil in autocorrelation (strictly, to the volume of
overlap, but for a cylinder-like function there is no difference), relative to the pupil area,
normalized to one. At the cutoff frequency - when the two centers are
separated by λfνC,
with νC=1/λF
and f the focal length (generally the image separation) - the two
centers are at the separation equaling pupil diameter.

Pupil function and, as expected, its
autocorrelation, becomes more complicated for aberrated systems.
Pupil function can be written as P (x,y)=T(x,y)ei2πW,
where T is the transmission over the pupil,
e is the natural logarithm
base, and W is the
aberration function expressing wavefront deviation in wavelengths (x, y
are the coordinates in the pupil plane). The factor
ei2πW
defines phase variation over the pupil in a complex exponential notation;
the reason it is the standard base for expressing complex numbers is
that
eix
function coincides with the wave cycle, i.e. describes a sinusoid that
repeats with the x+2π period.
These two parts of the pupil function are not directly compatible, with
the transmission T directly expressing field (amplitude) in the
pupil, and the phase factor
ei2πW
expressing the phase in the normalized 1 to -1 range. Given in units of
wavelength, W numerically corresponds to the phase angle φ
in units of the 2π
(radians) full phase, thus the identity
ei2πW=eiφ=cosφ+isinφ
effectively gives the two coordinates (it's never a sum) determining the
corresponding phase angle φ in the unit circle, as illustrated
below (while this phase angle could also be expressed using ordinary
numbers, the complex exponential form is generally preferred for ease of
calculation and versatility).

This phase factor of the pupil
function can be converted to the resulting amplitude at the focus point,
in proportion to cos(OPD2π/λ),
which is then describing the profile of pupil function. This is
illustrated for primary spherical aberration, best focus location, for primary
spherical aberration, 1/4, 1/2 and 1 wave P-V in magnitude (bottom; since OPD for primary spherical is described by x4-x2, which for the maximum deviation for x=0.707 gives -0.25, it in effect represents 1/4 wave error). For the wavefront error W=0, pupil phase factor is 1, the entire pupil is in phase, hence can be represented as a cylindrical volume of the height determined by the (unit) amplitude A. With 1/4 wave of spherical aberration, all points except the center and edge are out of phasen, with their amplitude contribution depending on the phase difference (for 1/4 wave, or π/2, difference, at the 0.707 zone, the combined amplitude with chief ray wave is 0.5, as illustrated below graph at left). At 1/2 wave P-V, amplitude drops to zero for the 0.707 zone (as well as the square of it, the energy). At 1 wave P-V, the 0.707 zone is back to unit amplitude. Pupil amplitude profile represents the amplitude contribution from every point of the pupil, but it is different from the combined amplitude (with coherent light), or combined energy (incoherent light)
at the focus location, which equals the sum of contributions from all points.
The transfer
function in incoherent light (OTF) for aberrated pupil can be also derived from the pupil
autocorrelation integral, i.e. as the common volume shared by two
identical pupil functions as one of them shifts to the right. The
starting point, when the two coincide, is zero frequency, and the cutoff
is when the two are only touching.
Therefore, a change in pupil function results in transfer function
change (aberrated pupil will, of course, impair coherent amplitude
transfer as well), generally impairment, and it is only logical since
amplitude spread function (ASF) and its squared modulus (magnitude), the
PSF, produced by the pupil are also changed (and also generally to the
worse). There is no simple explanation as to why is the field
(amplitude) diffracted to infinity (and brought to the image plane by
lens focusing) at the exit pupil proportional to the Fourier transform
of the pupil function - which is, proportional to its frequency spectrum
- but the cause is ultimately in the wave nature of light. Similarly,
OTF is the Fourier transform of the PSF, itself proportional to the
squared ASF. Shown below are these and some other Fourier pairs. Any
such pairs are merely two different forms of representing one same wave
phenomenon: one in the spatial/time, the other in the frequency
context.
 Left
side shows a function describing field in the exit pupil in terms of its
spatial properties, i.e. period and amplitude. At right is the
corresponding Fourier transform, as the spectra of specific sinusoidal
frequencies with specific amplitudes which, when summed up, produce the
pupil field function. Inset with each function illustrate its 2-D
intensity distribution (basically, top view of the 3-D function
distribution). Left
side shows a function describing field in the exit pupil in terms of its
spatial properties, i.e. period and amplitude. At right is the
corresponding Fourier transform, as the spectra of specific sinusoidal
frequencies with specific amplitudes which, when summed up, produce the
pupil field function. Inset with each function illustrate its 2-D
intensity distribution (basically, top view of the 3-D function
distribution).
For a point pulse in the pupil, Fourier transform is a constant
over all frequencies, i.e. the field at infinity has constant amplitude
(plane wave). Sinusoidal pupil function produces a 3-point actual
pattern, but the Fourier transform does not include the brightest,
central point (zero-order, i.e. zero-frequency term, called DC term,
expressing average brightness for all points; for the sinusoid shown,
centered around horizontal axis, the average of positive and negative
amplitudes is zero, but the energy is, of course, always positive and it
appears in the actual image) only the points generated by the two
first-order terms. The square wave amplitude pattern in the
spatial domain transforms into a line of discrete points diminishing in
brightness toward higher frequencies, with their amplitudes contained in
a sinc function envelope (these points of light, if sufficiently
magnified, will show the familiar point-image diffraction pattern). With
either sinusoidal or square wave, the increase in spatial period results
in shrinking of its frequency spectrum (i.e. shift toward lower
frequencies) i.e. narrowing in the separation between bright point in
the actual image of the transform. The square pulse function -
which is the central cross section of the aberration-free pupil function
- has as its frequency transform sinc function (shown is the relation
between the spatial period a and frequency for square aperture;
for circular aperture sinc function hits first zero at 1.22/a). Fourier transform of
a triangular pulse is sinc2,
i.e. the square aperture PSF (either shape is slightly different for
circular aperture). The corresponding intensity is proportional to this
transform squared, i.e. to sinc4,
which implies significant further weakening of the ring structure, i.e.
profile closer to Gaussian. Gaussian pulse transforms into
another Gaussian. Similarly to the discrete Fourier transforms for
periodic functions (sinusoid, square wave), increase in the pulse
spatial period (i.e. in the pupil diameter) results in shrinking of its
frequency spectrum, i.e. shrinking of the corresponding intensity
distribution of the field diffracted to infinity (or brought to a finite
distance by a focusing lens), and the other way around.
All this can be summed up as shown below.
With either coherent or incoherent light, it starts with pupil function
(in this case for circular aberration-free aperture), whose Fourier
transform - the amplitude spread function (ASF) - is the system's
impulse response for coherent light.
Pupil function along any single diameter is the square pulse, and for
the full circle it is a cylinder, with unit amplitude over pupil area,
and zero outside of it (the pulse and cylinder are referred to as 1-D
and 2-D pupil function, respectively, not because they themselves are
1-D and 2-D, but because they originate from 1-D and 2-D pupil
elements). For incoherent light, system
impulse response is the squared modulus (magnitude) of ASF, the point
spread function (PSF). The image in real space is formed by convolution
of the Gaussian image and system impulse response. In the frequency domain,
both object and image have their frequency spectrum - as the Fourier
transform of their respective intensity functions - with the image
spectrum being a product of object frequency spectrum and the transfer
function. The transfer function itself is merely the scaled version of
pupil function for coherent light, and pupil autocorrelation for
incoherent light.

In effect, the system impulse response acts
as a smoothing spatial filter, softening edges, reducing amplitude, and
suppressing high frequency distributions. In the frequency domain,
system's transfer function acts as a low pass frequency filter. It is
illustrated with coherent transfer function (top right) reducing
frequency spectrum of a periodic square wave to a single frequency,
whose inverse Fourier transform is the sinusoidal amplitude distribution
of the image.
Note that image formation in coherent light is in the context of
amplitude, since amplitudes of coherent waves add up directly as the
convolution of the system's ASF and Gaussian amplitude image, and it is
the resulting complex amplitude squared that determines the intensity.
With incoherent light, the phase of individual waves is not correlated, and
they add up their intensities directly, as the convolution of the system
PSF and Gaussian image. Only for point source there is no difference in
image formation in coherent vs. incoherent light (as long as it concerns
the relative, not absolute intensity distribution). The PSF is the Fourier
transform of the OTF, which means that it represents the amplitude
distribution resulting from OTF-like pulse. Its intensity is the PSF
squared, i.e. the 4th power of the ASF, with the ring structure nearly
vanishing (as it is to expect, with the OTF-like pulse having in general similar shape to the Gaussian pulse (i.e. central maxima steadily
diminishing toward zero going away from it), whose Fourier transform is another
Gaussian.
As mentioned before, the coherent transfer
function (ATF) formalism expresses only the transfer of wave amplitude
(i.e. field), and does not supply information about the image itself, as OTF
does. Thus, despite the ATF indicating that
the coherent light imagery is perfect for the range of frequencies lower
than 1/2λF (inverse linear frequency, with linear frequency given as a product of angular frequency in radians with the focal length), incoherent imaging is generally
preferable over the entire range of frequencies.
And, as illustration shows, the imaging
setup is relevant for microscopy, not astronomical observations. In the
optical telescope, image plane and focal plane practically coincide, and
the Fourier transform would have been taking place in the image, as
coherent spread functions
(CSF) created by light emitted from each object point and diffracted at
the telescope entrance pupil, interfering in the image at the amplitude
level. But even with near monochromatic (i.e. temporally coherent)
light, spatial coherence in the visual astronomy is only possible over very small, near
point-like patches. Extending size of the emitting area rapidly makes
light spatially incoherent. Thus, ATF is even less relevant for
astronomical imaging, where coherent light may be encountered only on a
very small angular scale, and image forming is subject to CTF amplitude
interference.
◄
6.6.1. MTF - aberration compounding, CCD, limitations
▐
7. OBSTRUCTION EFFECTS
Home
|
Comments
|