◄ 8. REFLECTING TELESCOPES   ▐    8.1.2. Newtonian collimation ►

The dominant off-axis aberration in the Newtonian is coma; astigmatism is low in comparison. Image surface deformation is field curvature, with distortion being zero with the stop at mirror surface. All three aberration are independent of mirror conic, which means that they are equally affecting both types of the Newtonian telescope, those with spherical and those with paraboloidal primary. Following are relations specifying the aberrations.

● lower-order coma, from Eq. 12-13 and 15.1, after substitutions, as the P-V and RMS wavefront error at diffraction focus for object at infinity is given as:

respectively, with α being the field angle (α=h/f, h being the linear height in the image plane, and f the mirror focal length). Note that this is double the error given by Eq. 12, which expresses only the peak aberration.

In units of the λ=0.00055mm wavelength, the coma wavefront errors are, slightly rounded off:

for D and h in mm (or with the numerical factor 38 and 6.7 replaced by 965 and 170, respectively, for D in inches).

For the 0.80 Strehl ratio, ωλ=1/√180, which corresponds to the field angle α=F2/90D in radians, for D in mm (α=F2/2286D for D in inches), or the linear height in the image plane

in radians, or α'=38F2/D in arc minutes, for D in mm (α'=1.5F2/D for D in inches). Evidently, unlike the linear quality field, which only changes in proportion to F3, quality angular field changes in proportion to F2 and in inverse proportion to the aperture diameter D.

As Eq. 70 implies, the wavefront error of coma in the Newtonian is inversely proportional to the square of its f-ratio for given angular field radius, and to the third power of it for given linear field radius. Thus it decreases exponentially with the increase in focal ratio, as illustrated on a simplified scheme below.

Also, Eq. 70 shows, coma of the concave mirror is independent of its conic. It, however, changes with the stop position and object distance, as described in 2.2. Coma (it also contains specifics on the geometric, or ray aberration). In terms of object distance O and mirror radius of curvature R, the coma wavefront error changes in proportion to (O+R)/O, with R being, according to the sign convention, negative. Thus, mirror coma diminishes with the object distance, falling to zero for object at the center of curvature (O=-R).

From Sa=5, the eyepiece focal length needed to enlarge the actual comatic image of a bright star with this amount of coma to 5 arc minutes apparent size, is approximately fe~1.4F. Hence an average observer, with a 5.6mm eyepiece and an f/4 mirror, can expect to notice coma on bright stars from ~2mm off-axis out. This corresponds to larger than 20° field angles, as in the above consideration; the difference is that the implication here is that the shorter f.l. eyepieces would not show edge coma due to the diminishing actual deformation of the central maxima at the image height they reach.

With an f/6 mirror, it will take an 8.4mm eyepiece to show the coma becoming apparent from some 7.2mm off-axis (which, from ε~57.3h/fe, fe being the ep f.l., would require 80+ degrees distortion-free AFOV); higher magnification will reveal little of the characteristic comatic deformation inside 7mm off-axis, due to the deformation becoming less apparent with the decreasing wavefront error. Compromised image sharpness, however, will be noticeable well within the 7mm-radius field circle (FIG 115, bottom).

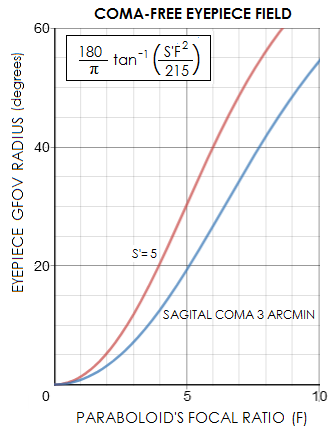
Due to eyepiece astigmatism, which increases with the square of eyepiece field angle, comatic-like deformation in the eyepiece grows rapidly toward the field edge. For given linear field radius in the image plane, eyepiece astigmatism increases in inverse proportion to the square of the focal ratio as transverse aberration (i.e. ray spot size) and inversely to the cube of it as wavefront error (lens astigmatism, given by Eq. 22, increases with the square of entrance beam width, which is inversely proportional to mirror focal ratio, and inversely to lens' focal length, which is proportional to the mirror focal ratio for given aperture and nominal magnification). Therefore, its proportion to mirror coma at given linear field radius remains constant regardless of mirror focal ratio.

If we express the coma blur length (Eq. 17) in arc minutes, it comes to 645h/DF3. Angular size of this blur on the retina is multiplied by telescope magnification M, to 645hM/DF3. Setting 645hM/DF3=3, since it is the angular size at which an object begins to appear non-point like to the average eye (although shape recognition requires at least 5 arc minutes size), gives the field radius h at which angular size of the coma blur is three arc minutes as

h=DF3/215M.

Average P-V wavefront error of astigmatism in a conventional eyepiece is approximated by WA~0.02fe(α/F)2 in units of 550nm wavelength, where fe is the ep focal length, and α is the ep field angle (AFOV/2). Substituting α~57.3h/fe gives WA~66h2/feF2, with the astigmatism wavefront error relating to that of coma (WC=37.9h/F3, also in units of the wavelength) as 1.7hF/fe.

The combined visible blur size can be, at least roughly, approximated as larger than coma-alone blur by a factor of 1+(WA/WC). If we assume that only about the bright 1/3 of the coma blur (sagittal coma) is visible, which is most often the case (the exception are bright stars, especially in large apertures) then the combined blur is roughly three times smaller.

Graph below (FIG. 115, top) illustrates how the quality visual field in the Newtonian telescope varies due to coma alone, but it also outlines how the magnitude of astigmatism in conventional eyepieces affects the actual field. Note that D/M in the above equations is, for convenience, replaced by the pupil diameter P. FIG. 115 bottom illustrates quality of the field within which comatic deformation of stellar images is not detectable, but the aberration is still large enough to affect image contrast.

 The green plots on FIG. 115 top, for the field radius with the angular sagittal coma within 3 arc minutes, represent the field quality with zero eyepiece astigmatism. The red plots, for the entire coma blur (tangential coma) are probably more representative with respect to the actual blur size, at least as a rough guide, considering that eyepiece astigmatism commonly enlarges the final blur. Somewhat larger blur, 3-5 arc minutes is still acceptable, and toward field edge, as much as 6-9 arc minutes is tolerable.

Expectedly, apparent size of the comatic image is in inverse proportion to the exit pupil size, i.e. relative telescope magnification. But it doesn't translate into inferior field performance. For instance, at the exit pupil diameter P=1 and f/5, coma blur reaches 3 arc minutes at nearly 0.6mm off axis. However, the corresponding error is still more than twice smaller than "diffraction limited". Since 1mm exit pupil at f/5 requires 5mm f.l. eyepiece (i.e. f.l.=F), its field radius at a standard ~45° AFOV is ~2.1mm, implying that roughly the inner half of the field area (~3/4 of the field radius) will be better than diffraction limited. At the very edge, coma is only about 1/3 larger than diffraction limited, or about 0.55 wave P-V, with the angular size of about 10 arc minutes.

On the other hand, at three times lower magnification (P=3), the 3-minute coma blur field radius also triples, to 1.8mm, with the coma this far off now somewhat worse than diffraction limited. At the field edge (assuming the same ~45° AFOV), it is as much as 1.9 wave P-V, or 10 arc minutes, same as at 1mm exit pupil. The difference is that both, comatic pattern deformation and energy lost to the rings are significantly greater at 1.9 than at 0.55 wave P-V. In other words, coma alone is more noticeable and detrimental at the lower magnification.

Plugging in the eyepiece astigmatism factor, with the astigmatism P-V wavefront error approximately  WA~1.7hWC/P, where h is the field radius and WC the P-V wavefront error of coma, makes the actual blur larger. At 1mm exit pupil (P=1), edge coma at h=2.1mm is about 0.55 wave P-V, implying about 2 waves P-V of eyepiece astigmatism; at 3mm exit pupil (P=3), h=6.2 and WC=2, implying as much as 7 waves of astigmatism. In both cases eyepiece astigmatism dominates mirror coma by roughly the same ratio, about 3.5 (eyepiece astigmatism for given field angle increases with the focal length, and coma increases with the image field radius), but both coma and astigmatism are significantly larger at lower magnification. Using

Bcomb=[1+(WA/WC)]BC

approximation for the combined geometric blur, with BC being the coma blur, gives that the combined edge blur for for both, 1mm and 3mm exit pupil is over four times greater than that for coma alone. That comes to over 40 arc-minute blur, more than the naked-eye full Moon. Of course, not all of it is visible, even with bright stars; roughly, only about 1/3 of it, or less, can be seen. That is still nearly half the full Moon diameter; since in both cases the eyepiece astigmatism is strong, and by nearly the same ratio so than coma, degree of deformation of the actual pattern is similar in both cases, resembling the right most pattern above, with somewhat flatter base and a fainter triangular tail.

The difference is that the blur size relative to the Airy disc is three times smaller at 1mm exit pupil, since at 1mm exit pupil everything is three times more magnified than at 3mm. So, while the apparent size of stellar images is similar to that at 3mm exit pupil, energy concentration vs. image scale at the higher magnification is significantly better, and the bloated outer-field stars are roughly three times smaller relative to near-perfect mid-field stars.

The 1 wave P-V wavefront error of coma is characterized by Sidgwick as limit to tolerable, visually. Obviously, it may not be so at high enough magnifications, and/or with significant eyepiece astigmatism present. In a 200mm f/5 Newtonian, coma is that strong at 3.3mm off axis. In the 10mm f.l. eyepiece, tangential coma is already 8.5 arc minutes, and sagittal near to 3. Average eyepiece astigmatism P-V wavefront error at this field height (close to 20° field angle) is nearly three times stronger than coma's, enlarging sagittal coma to roughly 11 arc minutes - quite obvious for most observers.

Summing it up, stellar deformation due to coma is not apparent at any magnification within field radius less than three times the diffraction-limited coma field. The field radius at which coma becomes apparent, if sufficiently magnified, is given by F3/30 in mm, or tanα=F2/39 angularly, with the magnification needed to make it apparent to the eye (~5 arc minutes sagittal coma) being provided by an eyepiece of 1.4F mm focal length. This assumes negligible eyepiece astigmatism. With conventional eyepieces, stellar deformation in faster mirrors will progressively more deteriorate toward the outer field due to eyepiece astigmatism. For instance, linear field radius at which stellar deformation becomes apparent is more than three times larger at f/6 than f/4, but the corresponding angular radius in the eyepiece magnifying it to 5 arc minutes is only about twice larger at f/6 (FIG. 115 top right). Thus the astigmatism at f/6 is effectively somewhat more than doubled at twice the angular radius (quadrupled due to doubled apparent angle, and larger by a factor 1.5 due to larger e.p. f.l. but more than halved due to the slower focal ratio), while at f/4 it is quadrupled, and combined with twice larger coma.

● lower-order astigmatism, from Eq. 18, after substitutions (for θ=0), as the P-V and RMS wavefront error at the best focus, for object at infinity, are:

with f being the mirror focal length.

In units of the λ=0.00055mm wavelength, the errors are:

for D in mm (or with the numerical factor 227 replaced by 5766 for D in inches).

The field angle at which astigmatism reaches 0.80 Strehl is α=√F/622D in radians, or at the off-axis height in the image plane of h=αf. It has no significance, with the coma error being absolutely dominant at this field angle. The two aberrations' RMS wavefront errors equalize for the field angle α=1/6F in radians, or for the h=D/6 height in the image plane, after which the astigmatism quickly becomes the dominant aberration.

The wavefront error doesn't change with object distance. However, it does change with the stop position. More details on this, as well as on the geometric (ray) aberration in 2.3. Astigmatism.

● field curvature: Petzval curvature of a concave mirror is Rp=R/2, R being the mirror radius. Due to the presence of astigmatism, actual best image curvature is different from the Petzval. Also, it varies with the stop position. For the stop at the surface, best, or "median" image surface equals the negative of mirror's focal length:

which makes it positive (concave toward mirror) for mirror oriented to the left, regardless of mirror conic. Position of the aperture stop influences mirror astigmatism, which in turn causes changes in the median image curvature. As Eq. 39 shows, it varies somewhat with the conic. For a paraboloid, best image surface is flat with the stop at half the focal length from mirror, and with the stop at the focal length away mirror astigmatism is cancelled, but image curvature equals R/2 (convex toward mirror). For a sphere, best astigmatic field is flat for the stop at (1-0.51/2) focal lengths from mirror, and astigmatism is cancelled for the stop at the center of curvature.

Miscollimation sensitivity of a Newtonian is determined by the diameter and F-number of the primary mirror. Sources of miscollimation are: (1) primary tilt/decenter, (2) flat tilt/decenter/despace, (3) focuser tilt/decenter and (4) tube/structural flow resulting in any of the former. As a result, axial image point is shifted away from the field center, and replaced with certain amount of off-axis coma.

Expressing the linear center field shift as 2τf/(60x57.3), for τ the mirror tilt angle in arc minutes and f the focal length, and substituting it for h in Eq. 70.1 (right), gives the RMS wavefront error of coma shifted to the field center (in units of 0.00055mm wavelength) as:

for the aperture diameter D in mm (for D in inches, ωt = τD/10F2).

Assigning H to the diagonal-to-focus separation, and H' to the focus height in the focuser (measured from the focuser base), the miscollimation sensitivity per arc minute of tilt is smaller by a factor H/f for the diagonal, and by a factor of H'/2f for the focuser, respectively, with f being, as before, the mirror focal length.

Sensitivity to decenter - also in units of 550nm wavelength - is identical for all three, mirror, flat and focuser, and given by:

for the decenter ∆ in mm. It is also the despace sensitivity of the flat for despace in mm.

More details on collimating Newtonian on the following page.
 

◄ 8. REFLECTING TELESCOPES   ▐    8.1.2. Newtonian collimation ►

Home  |  Comments