|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
6.4. Diffraction
pattern and aberrations
▐
6.5. Strehl ratio
► 6.4.1. Star testing telescope optical quality
PAGE HIGHLIGHTS As FIG. 96 shows, even a slight presence of any wavefront aberration changes the form of diffraction pattern, leaving its unique fingerprint on it. With the knowledge of what those fingerprints look like, with some practical experience, the aberrations can be detected and, most often, quantified with sufficient accuracy. Thus, all that is needed to test telescope optics for quality is a single point-source of light. It can be either a star, or a small, man-made source of light that fits the definition of a point-source. The telescope should be well collimated, and in thermal equilibrium with surrounding air (depending on the telescope size, type and initial differential, it can require anything from minutes to hours). In order to visually analyze diffraction pattern, it has to be sufficiently magnified. Minimum magnification for conducting star test is considered to be 25x per inch of aperture (or equal to the aperture diameter in mm), but more is better. Optimum magnification level is probably between 40x and 50x per inch, combined with moderate defocus, of between 3 to 5 waves (number of rings in the defocused pattern roughly corresponds to the defocus in waves). When testing on a star, it shouldn't be too bright, nor too faint; either can hide more intricate, yet potentially important features of the diffraction pattern. Optimum level of brightness for a 6 inch aperture is ~2nd magnitude star, which helps define best star magnitude for the test, in terms of aperture diameter D, as m~5logD-8.9 for the aperture D in mm, or m~5logD-1.9, for D in inches. Test star should be close to zenith, to minimize the effect of seeing, although for telescopes without tracking mechanism Polaris may be the best choice most of the time. Needless to say, less than good seeing quality will compromise reliability of star test results (steady air is also required for artificial star testing; no heat radiating object or areas should be close to the light path). When star testing with an artificial star, two more requirements have to be met: (1) angular size of the light source needs to be less than 1/2 of the Airy disc size, and (2) distance between the source and the telescope needs to be large enough to keep spherical aberration induced by the finite object distance negligible. The first requirement demands the artificial star to be what it needs to be for the test: effectively a point source of light. Diffraction theory shows (Optical Imaging and Aberrations 2, V. Mahajan, p214), that if the source diameter exceeds 1/4 of the Airy disc's, resulting diffraction pattern begins to change: its full width at half maximum (FWHM), first minima radius and overall ring structure all become larger. At the source diameter of 1/2 the Airy disc's, the FWHM is nearly 15% larger, with the first minima nearly doubling in radius (in effect, the first dark ring vanishes, with the central disc and first bright ring merging). At the source size equaling the Airy disc's, the FWHM is already 60% larger, and the in-focus ring structure diminishes further. There is no specifics on how it affects defocused patterns, but it is a common sense to try to preserve the form of diffraction pattern produced by artificial star closely resembling the one that we are comparing it to. With today's availability of materials and products, this shouldn't be an obstacle. Obviously, angular size of an artificial star is a function of its diameter and its distance from a telescope. Simple visualization of the Airy disc in the focus of a telescope, with two lines extending from its top and bottom to cross at the aperture stop and diverge outwards, helps define the size of Airy disc projection for any given distance from the telescope. Knowing that the Airy disc diameter in radians is given by 2.44λ/D, which for λ=0.00055mm comes to 1/745D for the aperture D in mm, linear diameter corresponding to angular Airy disc diameter at any distance L is given by S=L/745D. Since we want to be as close to an actual point-source pattern as possible, the target size for the artificial star is 1/4 as much, or S ~ L/3000D (note that L needs to be in the same measuring unit as D, here in mm). For instance, for D=100mm telescope, an artificial star placed at 50m distance shouldn't be significantly larger than 0.17mm in diameter. For distance L in feet, aperture D in inches, the maximum source diameter in mm is L/250D. It is a bit more complicated when it comes to determining artificial star distance that will not induce spherical aberration appreciably affecting test results. The complexity arises mainly from the great variety of different telescope systems in use today. While they are all optimized for object at infinity - or at least at a large distance - the amount of sensitivity to reduced object distance can vary significantly from one type to another. Some systems are easier to deal with, in a sense that they come with the basic specifications known and/or relatively constant. Some others have undetermined optical specs, thus cannot be predicted with respect to their specific object distance sensitivity. The easiest are single mirror systems: Newtonians with either paraboloidal or spherical mirror (diagonal, by definition, has no optical power, and its surface errors do not induce spherical aberration). For object distance in units of mirror's focal length L/f, and its reciprocal value ψ=f/L, the P-V wavefront error of spherical aberration at the best focus induced by object distance is given by a simple relation,
where K is the mirror conic, D the aperture diameter in mm, and F the focal ratio. The sign of wavefront error indicates the form of aberration; when the aberrated portion of the wavefront is closer to best focus than the reference sphere, it is over-correction, and vice versa. Therefore, the aberration induced is over-correction for K<-(1-2ψ)2. Taking relatively close object, at twenty focal lengths away (ψ=1/20), conics smaller than -0.81 will be inducing over-correction error, those greater than -0.81 under-correction, and the error will be cancelled for K=-0.81. With spherical mirror, there is no need to worry about the close object error; being under-corrected for object at infinity, and with closer objects inducing overcorrection, it actually becomes better corrected with reduced object distance. The closer object, the more so - up to the object placed at mirror's very center of curvature, where sphere provides perfect imaging. For testing purposes, however, it is good to know what level of error it should have - if it is really spherical. By substituting 0 for K in the above relation, the wavefront error is given as Ws=D(1-2ψ)2/2048F3. Deviation ratio δ of the actual vs. implied value indicates non-spherical surface, with its conic given as K=(δ-1)(1-2ψ)2. In other words, it is prolate ellipsoid for 0<δ<1 and oblate ellipsoid for δ>1 (negative δ value implies hyperboloid). Taking, for instance, δ=0.6, implies K=-0.324 for object at ten focal lengths away (ψ=1/10), and K=-0.361 for object at twenty focal lengths. The positive sign of δ implies that the actual error is under-correction, of the same sign as that of spherical mirror (which induces under-correction with any object farther away than its center of curvature). The same amount of over-correction error - thus resulting in a negative ratio value - would imply the corresponding conics -1.296 and -1.444, respectively (hyperboloids). The actual-to-ideal δ value of 1.4, on the other hand, implies K=0.324 and K=0.361, respectively (oblate ellipsoids). For a paraboloid, which is axially perfect for object at infinity, there is a price to pay with closer objects and the currency is over-correction. Substituting K=-1 in Eq. (a) gives Ws=(ψ-1)ψD/512F3, and neglecting the ψ term in the bracket (for any serious test, object needs to be significantly farther away than 10 focal lengths, which makes ψ significantly smaller than 0.1), it reduces to Ws~ψD/512F3. With ψ=f/L=FD/L, this gives Ws~D2/512LF2, and the object (i.e. star) distance in terms of the wavefront error as:
(all three parameters, D, W and L are in the same units). Since this value for the light source distance L is effectively based on the P-V wavefront error Ws larger by a factor 1/(1-ψ) than the actual error, it is larger by a factor 1/(1-ψ), or L/(L-f), than a distance corresponding to the actual Ws value. For the wavelength in units of 0.00055mm (and D in mm), test distance is L~3.55D2/WsF2. For L in feet and D in inches, it is L~7.5D2/WsF2. Substituting optional maximum tolerable P-V error of spherical aberration for Ws gives the appropriate minimum distance for the artificial star. For instance, by substituting W=λ/20=0.0000275mm for λ=550nm, gives the distance for this error level for D=400mm, f/4, as L=710m. As the original relation implies, the actual distance for that error level is smaller by a factor of (1-ψ) than that given by the approximation. That comes to 11% difference at a ten focal length distance, and 5% at twenty focal lengths. Nearly exact expression for the appropriate distance, for all practical purposes, is given by L=(1-ψ')D2/512WsF2, where ψ' is obtained from ψ'=f/L, using the distance L given by the approximation. Solving Eq. (a) for ψ gives the exact value as ψ=0.5-0.5(2048WF3/D)0.5, which is used to plot required distance for 1/20 wave P-V of spherical aberration as a function of mirror aperture diameter D and focal ratio F, shown below.
Required distance ranges from 5.5m with a 100mm f/10 and ψ~0.18 (1/0.18=5.5m), to 2km (1.24 mile) with 500mm f/3 paraboloid and ψ=0.00075 (1.5/0.00075=2000m). The distance scales inversely to the wavefront error, so half as large error (1/40 wave P-V) would require doubling the distance. Obviously, required artificial star distance becomes impractical for larger, fast paraboloids. Is 1/20 wave error tolerance really necessary? It is; moreover, it may be still to much. For instance, if a mirror is 1/6 wave P-V inherently over- or under-corrected, a 0.05 wave of over-correction induced by the object distance would alter test result into -1/4.6 wave or 1/8.6 wave P-V, respectively. For accurate star testing, the error induced by object distance shouldn't significantly exceed 1/50 wave P-V. This pretty much rules out an artificial star test for larger Newtonians.
Catadioptric
Newtonians with full-aperture Maksutov or Schmidt corrector can be
significantly less sensitive to reduced object distance than
paraboloidal Newtonians. Catadioptric
two-mirror systems are not uniform enough in their production types to
fall under some type of generalization. Image below should give an idea
of the error induced by object distance for the several most common
systems. The error scales with the aperture (it is given as RMS
wavefront error, since in the presence of central obstruction the
P-V error given by raytrace, due to the manner of calculation, is
nominally inflated; in addition, systems employing Maksutov corrector
usually have a mix of supposedly balanced 6th and 4th order spherical
aberration, having different P-V to RMS ratio than primary spherical).
An 8-inch SCT, regardless of the modality (standard, w/aspherised
secondary, or Edge) will have about 1/4 wave P-V worth of overcorrection
with object placed at ten focal lengths away. The error scales inversely
with the distance. Maksutov-Cassegrain configurations, in general, have
similar sensitivity to object distance. With standard focusing,
the error is likely to remain acceptable within the focuser range.
With fixed focus (i.e. mirror focusing) the induced error is undercorrection,
and ranges from near-negligible for systems with aspherized primary,
even with light source as close as 10 focal lengths away,
to roughly comparable to that of an SCT with all-spherical systems.
Similarly, Maksutov-Newtonian at f/6 is practically insensitive
to object distance within its focuser range, and even with an extender.
The Schmidt-Newtonian, at f/4, is more sensitive: in order to keep the induced error
at 1/20 wave P-V (0.015 wave RMS) a 200mm f/4 system needs object
to be 35 focal lengths away. A 6-inch f/6 Schmidt-Newton - to make
it directly comparable to the Maksutov-Newton - would have 1/20 wave P-V
worth of overcorrection at the object distance of 9.3 focal lengths.
The corresponding focus extention with respect to object at infinity
would be 92mm. And vice versa, a 200mm f/4 Maksutov-Newtonian would
generate 1/20 wave P-V of undercorrection (not a typo, Maksutov systems
tend to generate undercorrection, as opposed to overcorrection of the
Schmidt systems) at the
object distance of 49m, or 60 focal lengths - significantly more than
for 200mm f/4 Schmidt-Newton. The likely reason
Maksutov-Newton is significantly more sensitive than Maksutov-Cassegrain
varieties is that the meniscus is sensitive to ray geometry:
the former has significantly shorter focal length, hence the
actual object distance is as much smaller.
For all-reflecting two-mirror systems, close object error of spherical aberration is given by Eq. 92 (also plots for the three most common systems), and for the typical commercial SCT by Eq. 120.3. Ordinary
doublet achromat is very tolerant to the reduction in object distance in
focal ratios ~f/10 and slower.
A 100mm f/10 achromat will likely generate about 1/20
wave P-V of under-correction with the object (artificial star) as close
as 10 focal lengths away (given relative aperture, the error level is
nearly in proportion to the aperture size). On the fast end, however,
the sensitivity can be several times, or more, greater. A 4 inch
f/6 achromat
can generate in excess of 1/5 P-V of under-correction with the object at
10 focal lengths away, due in part to the generated lower-order
aberration falling out of balance with the higher-order component (the
error is nearly inversely proportional to object distance). This
aberration duality makes the sensitivity of these instruments to object distance fairly
unpredictable, because the level of higher-order aberration and
proportion of
balanced lower- and higher order spherical aberration vary from one system to another. Similar applies to
apochromatic refractors. Since an object at 10 focal lengths away
will extend the focal length by a 10/(10-1) ratio,
most focusers wouldn't be able to accommodate needed refocusing.
A standard 100mm f/8 apo
(ZK7/FPL53) would generate 0.073 wave RMS
- nearly 1/4 wave P-V equivalent - and a 110mm f/6 triplet, with
practically zero P-V wavefront error at infinity focus,
0.28 waves P-V (0.085 wave RMS) of undercorrection with object at
10 focal lengths away. DIFFRACTION PATTERNS Proficient star testing requires the ability to properly interpret diffraction pattern seen in the eyepiece. Familiarity with the characteristic forms associated with particular aberrations is easiest to acquire by way of software-generated visual simulations. While the actual testing commonly involves more complex pattern forms than those caused by a single aberration, knowledge of the single-aberration patterns is always the starting point. Following simulations are generated by Aberrator (Cor Berrevoets), except the zonal error, which is generated by Aperture (Harold Suiter). Shown are all common conic surface aberrations, at the level of 0.80 and 0.95 Strehl, for unobstructed and 0.3D (30% linear) obstructed aperture. Light travels from left to right, thus defocus in the intrafocal direction is numerically negative, and positive for extrafocal direction (patterns are given for defocus values -4, -2, 0, 2 and for waves, since this range of defocus is generally the most sensitive for detecting aberrations). Axial cross section is not commonly presented, but it helps better understand how particular patterns form.
Similarly to the primary aberration,
shown is "overcorrection" for the balanced secondary spherical aberration, with the outer rays focusing behind
paraxial focus. For "undercorrection", the patterns are reversed.
Mainly due to its somewhat different wavefront deviation form,
namely additional "wrinkle" at the edge, throwing light out at a
greater angle, the intra- and extrafocal patterns differ more than
with the primary spherical. In unobstructed aperture, the tail tale
sign can be a pair of equally bright rings in the focused pattern,
but the aberration is even easier to detect than the primary form,
either at the 0.95 Strehl level (0.20λ
P-V), or the "diffraction-limited" 0.80 Strehl (0.40λ
P-V, 0.075λ
RMS).
The 0.37λ
P-V wavefront error of primary astigmatism (0.0745λ
RMS), resulting in 0.80 Strehl, is easily detectable in both,
focused and defocused patterns. In the former by the first bright ring
morphed into a cross-like pattern around the central maxima, and in the
latter by elliptical elongation of defocused patterns, with the
orientation perpendicular one to another for the two opposite sides
of defocus. At twice lower nominal wavefront error it is, however,
harder to detect than spherical aberration; it could give only a
hint of the cross-like change in the ring form with bright stars.
Unlike the other three aberrations, primary coma
has identical patterns on either side of defocus. It is the
consequence of its wavefront deviation shape, which has one half of
it flatter, and the other more curved to identical degree. Hence the
former focuses as much longer, as the other focuses shorter, with
the identical angles of conversion, only of opposite sign (in this
particular pattern, the top half of the wavefront focuses farther,
and the bottom half closer). Luckily, it is the easiest to detect in
its focused pattern. Its "diffraction limited" level, 0.80 Strehl, and 0.0745 wave RMS, is at 0.42 wave P-V. Even at the 0.95 Strehl level (0.21λ
P-V), one side of the first bright ring is noticeably brighter and easy to detect even in moderate seeing (assuming, of course, bright enough telescopic star). This allows for very accurate collimation of telescopes with inherent coma.
These patterns illustrate the effect of
zonal error. The zone generates 0.075λ
RMS wavefront error (WFE), thus produces 0.80 Strehl. To some
extent, it resembles spherical aberration (it is a raised zone,
focusing behind paraxial focus, thus resembling overcorrection),
in that it has brigther inner pattern area on one, and brigther
outer pattern area on the other side of defocus, but unlike
spherical aberration, has a distinctive double ring in addition
to the first bright ring in the focused
pattern. With obstructed apertures, it is possible
that zonal deformations could aslo, similarly to primary spherical
aberration, be approximately quantified looking at the defocus
distance at which the shadow breaks out, at least for some
specific forms of zonal deformation.
As mentioned, actual instrument will most often have a
mixture of different aberrations. Characteristic patterns for some other
aberration forms are given in
FIG. 96.
Some aberrations, like axial astigmatism, pinch deformations, or tube
currents will affect the form of defocused patterns, but have little
effect of intensity distribution, allowing for the spherical
aberration level estimate - as long as they are low in
magnitude. However, circular zonal surface deformations
will affect intensity distribution within defocused patterns, possibly
significantly, making the accurate estimate of spherical aberration
level challenging.
Turned edge effect
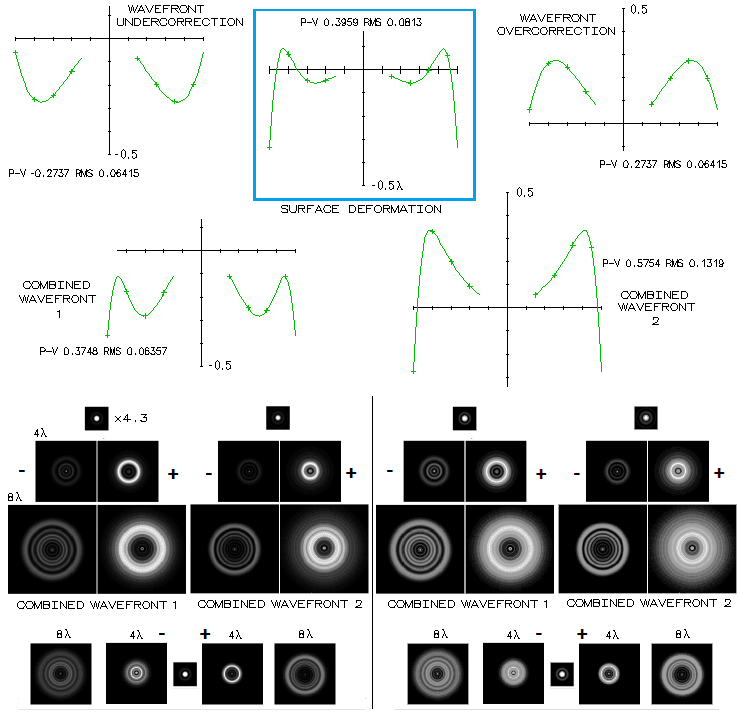
As an example, surface deformation created by
combining higher order aspheric terms so that it resembles turned
down edge, is combined with λ/4 wave P-V of primary spherical aberration
(below; in the blue box is the wavefront deformation due to TE, at its best focus). Roughly, it should illustrate the effect of λ/2 wave
TE starting at ~0.92 zone on defocused patterns with λ/4 wave
P-V of primary spherical aberration (the RMS wavefront error for the TE shape is
inflated due to the relatively large P-V error limited to a relatively small
wavefront area, indicating 0.74 Strehl,
while the actual is 0.79). The effect is dependant on the
sign of deformation vs. sign of SA, hence it is shown with both,
undercorrected and overcorrected wavefront (note that OSLO has different
sign convention for the wavefront error sign, opposite to the standard convention).
The mirror induces slightly less than λ/4 P-V wavefront
error of spherical aberration, but with 25% (linear) central obstruction
it is somewhat lower, at 0.065 wave RMS (corresponding to λ/4.6
wave P-V; the P-V error displayed by OSLO is measured from the virtual
wavefront vertex, hence larger than the actual one). As the OPD plots
for combined wavefronts show, undercorrected wavefront has the error
reduced, while the overcorrected one has it increased. The two combined
wavefronts differ not only in magnitude, but also in their shape: the
former is similar to that of nearly balanced 6th/4th order spherical,
while the later is a combination of defocus with a very pronounced turned
edge of opposite sign.
As a result, defocused patterns for the same amount of primary
spherical differ for undercorrection (left) vs. overcorrection (right),
as well as those two vs. that same amount of spherical aberration
without presence of TE (bottom). On the left half, there are diffraction
patterns as displayed by OSLO Edu, with linear intensity scaling,
and on the right toward natural, logarithmic scaling (it reminds
that the telescopic star brightness also can significant effect on the
pattern appearance). The "-" sign indicates inside focus. In general,
circular zonal surface deformations either add or subtract from wavefront
deformation caused by spherical aberration, but likely altering its
textbook form. As a result, intensity distribution also changes, and when it does,
it is most readily visible in the defocused patterns. In order to have
significant effect, such deformation has to be large enough in magnitude,
relative to that of spherical aberration. Harold Suiter's "Star Testing Astronomical Telescopes" discusses in details star testing, connecting it to the underlying optical theory. An interesting new development (relatively speaking) is Roddier's test, (freeware) which uses CCD image of two defocused diffraction patterns of a real star to determine wavefront quality (seeing effect is averaged out through the exposure length, and also relatively insignificant, due to the large size of defocused patterns). FOUCAULT STAR TESTIn addition to directly looking at the star image, star testing telescope optical quality can be conducted by using a straight edge cutting into the focus of the objective. Unlike the standard star test, which generally needs defocused patterns in order to form conclusions, it is a null test, that can indicate level of aberrations present at a single focus location. Simulated patterns below ("Diffract" by Jim Burrows) illustrate test capabilities.
On the left are nulls for isolated aberrations, primary spherical, astigmatism and coma, and on the right spherical aberration mixed with either one of the other two. Top right shows null for the paraxial, best and marginal focus in the presence of 1/4 wave P-V primary spherical. Simulations suggest that this form of star test has higher sensitivity to these aberrations than either standard Foucault, or Ronchi test, and in some aspects, possibly, even the standard star test. RONCHI STAR TESTAnother possible modality of the star test is use of the Ronchi grating at the focus of the objective. Similarly to the standard star test, defocused patterns are necessary for evaluation of the aberration level. Simulations below ("Diffract", Jim Burrows) illustrate test's capabilities.
Sensitivity of the test is higher for slower systems, and for higher line density. Commercial "Ronchi eyepiece" made for this purpose has 250LPI density, but it could be made out of any eyepiece simply by inserting Ronchi grating at its field stop location (grating line can be used as a straight edge for the Foucault star test). Simulations indicate that the Ronchi star test has overall sensitivity inferior to the Foucault, or the standard star test. Yet, with 250LPI grating density (or less with slow systems), it can be of practical value either as stand-alone, or a complementary test. If a star is left to drift across the grating, it can reveal local wavefront irregularities with accuracy in both, location and amplitude, not possible with other tests. In conclusion, it appears that the Foucault star test deserves more attention and use. It is relatively insensitive to the focal ratio and, as the only null test of the three, simple to conduct and interpret. It can detect low but not negligible astigmatism in any orientation, as well as coma, with only a single test image to evaluate. And, since it doesn't require nothing in addition to what the standard and Ronchi test do, there is no reason not to have all three of them at disposal, and use them as needed. Follows more detailed
description of the Strehl ratio and MTF. ◄ 6.4. Diffraction pattern and aberrations ▐ 6.5. Strehl ratio ►
|