|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
10.2.3.5.
Maksutov-Cassegrain telescope off-axis aberrations
Off-axis aberrations
of the meniscus, unlike those of the Schmidt corrector, are not
negligible. Both coma and astigmatism of the meniscus are of the
opposite sign to those of the primary mirror, and of the same sign as
those at the secondary. Due to
the secondary spherical aberration contribution, also opposite to that
of the primary (for spherical mirrors), the meniscus in two-mirror
systems is somewhat weaker, thus also with somewhat lower contribution of
(opposite) coma and astigmatism relative to those of the primary.
The
primary
coma aberration coefficient
for the meniscus is, as
mentioned, approximated by cL~-1.2q/fL2,
q being the shape factor (R1+R2)/(R1-R2).
With q expressed in terms of the meniscus focal length fL
and first radius R1,
it can also be written as cL=
-1.2/R1fL.
The system coma coefficient is a sum of the contributions from the lens
and the two mirrors:
also for
spherical surfaces, with the values in the brackets, from left to right, being the aberration
contributions of the meniscus lens
cL, primary,
cP, and secondary,
cS, respectively.
As before, σ1 is the stop (corrector) separation from the primary
in units of the primary's r.o.c., k' is the relative height of
marginal ray at the secondary, m' is secondary magnification and
σ'2 the relative exit pupil separation
for the secondary, obtained from
Eq. 116.1 with σ1, k' and m'
substituted for σ, k and m, respectively (m', k'
and
σ'2 represent the final values of these parameters determined by
the corrector's
power, as explained with
Eq. 129).
Substituting for ρ=mk/(m-1) in Eq. 116.1 and neglecting the prime
notation for the parameter change due to the meniscus' power, gives
approximation σ'2~{k-[1/(1-2σ1)]}(m-1)/2mk.
Approximating σ1~(1-k)/2,
which is nearly exact for the Gregory-Maksutov, gives σ'2~[k-(1/k)](m-1)/2mk.
The system P-V wavefront error is given by
Wc=cαD3/12,
with α
being the field angle in radians. Expressing R1
and fL
in terms of the primary's radius of curvature RP,
the meniscus coma coefficient is approximated by cL~1.2t1/4/1.7RP9/4,
t being, as before, the corrector center thickness.
In terms of the coma of the primary mirror, for the typical relative
separation σ1~0.4, that gives cL/cP~|t/RP|1/4.
It shows that coma contribution of the corrector slowly increases with
its relative thickness. However, this doesn't take into account the weaker
corrector due to the presence of secondary mirror. With the secondary
spherical aberration contribution approximated with -1.2k (from
Eq. 154), in terms of the primary mirror
contribution, and the aberration contribution of the corrector changing
approximately in proportion to R14,
the front meniscus radius needed to correct the two mirror's spherical
aberration is weaker approximately by a factor of (1-1.2k)1/4.
Since the meniscus' focal length fL
changes nearly in proportion with R1,
it gives better approximation of the corrector coma contribution as
cL/cP ~ 1.2|t/RP |1/4(1-1.2k)1/2.
For the average |t/RP|~0.02
ratio and k~0.25 for MCT with separated secondary, the corrector coma contribution is nearly -0.4 of the primary's
(with the stop at the corrector),
increasing only about 5% for k~0.2. For the secondary coma contribution,
also in units of the primary's, substituting σ1~(1-k)/2
and σ'2~(m-1)/2mk2,
gives it as approximately cS/cP~(m-1)/(1+k)m. For the average k~0.25 and m~5 (σ'2=-7.6), secondary's coma
contribution is, from Eq. 131, about -0.63 of the primary's,
exceeding -0.7
for k~0.2, m~6 and σ'2~-10. Since
the secondary magnification m and relative minimum size k
are inversely correlated as a function of the back focal length, for the typical MCT
telescope the secondary
coma contribution quite simply can be roughly approximated by cS/cP~-0.32/√k.
The approximate coma contributions from the three MCT elements, as well
as the resulting system coma, as a function of the relative meniscus
thickness, are shown on FIG. 190.
FIGURE 190: Coma in the Maksutov
Cassegrain is a sum of the coma contributions of the primary, secondary
and meniscus. The secondary and meniscus induce coma of the same sign,
and opposite to that of the primary, with the system coma being given by
the sum of the three. For given meniscus thickness, the system coma
nearly entirely depends on the minimum relative size of the secondary (k).
Smaller secondary - hence generally higher secondary magnifications
needed for a given back focus - increases the relative secondary
contribution (in units of primary's contribution), as well as that of
the meniscus, but only to a small extent for the latter. The meniscus'
contribution increases more significantly with its relative thickness in
units of the primary's radius of curvature (Rp).
For the loose t/Rp
average of ~0.02, the near-zero system coma is indicated for k
slightly larger than 0.25 and the corresponding secondary magnification
of approximately 4 to 5. Due to the limitation imposed by its secondary
surface radius coinciding with the rear radius of the meniscus, the
arrangement with a silvered spot on the meniscus (Gregory-Maksutov)
requires higher secondary magnification - i.e. smaller minimum secondary
size - resulting in the larger system coma. In general, these systems,
if kept all spherical, cannot be coma-free, and the magnitude of coma,
as indicated by the graph is around 15% of the primary's. Note that this
is only for the lower-order (primary) coma. Secondary coma - originating
mainly at the meniscus, negative in sign - can become significant in the
systems with fast primaries. At f/3
primary it is roughly 10% of the primary's coma in magnitude, and will
add to the negative primary coma of the meniscus and secondary mirror.
The above indicates that the lower-order coma level
in the MCT is generally low, as long as the usual designing freedoms are available.
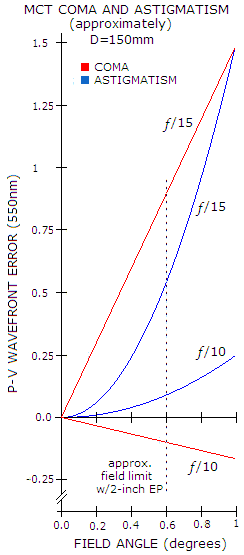
The coma is likely to be near zero for the f/10-11
systems, while larger and negative (tail down) with the slower
ones, with the coma coefficient ranging from near-zero positive (~3% of
the primary's, tail up) coma at f/10
to nearly 15% of the primary's coma (opposite in sign, i.e. negative) at f/15.
With the P-V wavefront error given by Wc=cαD3/12,
and the coma coefficient for a mirror with the stop at the surface given
by cM=1/R2,
becoming smaller by a factor 1-σ1
with displaced stop, σ1
being the stop (corrector) separation in units of primary's focal
length, taking 150mm aperture, σ1=0.4 and f/3
primary (so R=-900mm), the latter would come to 0.5 wave P-V (0.09 wave
RMS) for 550nm wavelength at 0.5° off-axis for f/15
system, and about 1/5 as much in an f/10.
In other words, lower-order coma is within diffraction limited over
0.4° field radius for the former, and about five times larger
radius for the latter.
However, higher-order
coma in the typical MCT is not negligible, and it combines with the
lower order form in producing the final magnitude of the aberration. It is mainly produced by the
corrector and negative in sign (tail down). This means that the two a smaller or
greater degree offset one another when the lower-order form is positive,
and add up when the lower order form is also negative. Going again from f/10
to f/15, the higher-order coma system coefficient increases by about
50%, from nearly twice the system's positive lower-order coma at f/10
(about 5% of the nominal primary's lower-order coma) to about one half
of the five times larger negative system coma at f/15. Most of the
increase is due to the stronger corrector needed to compensate for the
lower spherical aberration contribution of the smaller secondary.
In other words, higher and lower-order coma at f/10 partly offset one
another, with the ~80% higher order excess, resulting in the
predominantly higher-order form with nearly as large P-V wavefront error
as the lower-order form alone, only of opposite sign. That would make
the the combined higher and lower-order coma error in a
150mm f/10 MCT at 0.5° off-axis is nearly 1/10 wave P-V. Or, for all practical purposes, non-existent
(which is pretty much the case with the lower-order form alone).
Different story at f/15. Here, the lower and higher order forms are of
the same sign, and they are both larger than at f/10, particularly the
lower order form. The addition of the higher-order form increases the
combined P-V wavefront error by about 50%, bringing it to nearly 3/4 wave
P-V, or so, at
0.5° off-axis. However, the final error is is determined by the
magnitude of astigmatism.
Lower-order astigmatism in the MCT is also generally
low, but both, less predictable and potentially greater than either in
the SCT or Houghton-Cassegrain. The reason is that neither Schmidt nor
Houghton correctors have significant power, thus their astigmatic
contribution is negligible. On the other hand, Maksutov corrector has
relatively significant power and thickness, both resulting in a
potentially significant amount of astigmatism, opposite in sign to that
of the primary (hence of the same sign with the astigmatism of the
secondary). So while the effect of the corrector's position on primary's
astigmatism in a two-mirror system is
generally similar to that in a Newtonian-style Maksutov or Schmidt, due
to the stop (corrector) position relative to the primary being similar
(typically, σ1~0.4), the system error is different. If astigmatism of the two
mirrors nearly balances out, it leaves the meniscus' contribution as the
dominant in the final system error. While it is relatively low, even low-level astigmatism can significantly change
best field curvature, and also may become less than tolerable farther
off-axis. If the secondary astigmatism overpowers that of the primary,
combined with the meniscus' contribution it would likely result in a
more than insignificant system error. And vice versa, if astigmatic
contribution of the secondary is lower than that of the primary, astigmatism of the
corrector will play balancing role.
As mentioned in the previous section, aberration coefficient
of astigmatism for the Maksutov corrector is disproportionately greater
than its power, due to it being a strongly curved thick meniscus qs
illustrated at left.
Exaggeration of the effect of meniscus' thickness on its
astigmatism (simplified; the actual CR path is refracted, involving
meniscus' principal points, typically at a significant separation
from the meniscus itself).
While the effective focal length is relatively weak, both surfaces
are strongly curved, of high powers and, consequently, astigmatism.
As long as the meniscus is thin, their aberration nearly
offset due to similar opposite powers. As the lens thickness (t)
increases, the chief ray (CR) arriving at the front surface
at an angle α, arrives at the
second surface at an increasingly smaller angle α',
due to an effective rotation of the second surface around its center
of curvature C. The effective inclination angle α' at the second surface is given by
α'=α-β.
As a result, astigmatism at the second surface diminishes, which in
turn increases the total lens' (meniscus) aberration. Depending on
the system configuration, it may or may not be desirable.
While the aberration coefficient of astigmatism
for a thin lens is a=-1/2f,
f
being the focal length, Maksutov
corrector generates significantly more of the aberration, due to the
imbalance in contributions of the two surfaces caused by meniscus'
thickness (it also affects meniscus' coma, but to a lesser degree, due
to it changing with the angle, not the square of it). Astigmatism added due to
the meniscus' thickness, in a form of the aberration
coefficient, is a'=t/2f1R2,
with f1
being the first surface focal length. System coefficient of astigmatism is
approximated by a~(n2+n-1)(n-1)t/2n2R1R2.
Most of its numerical value comes from the portion caused by lens thickness,
which can be written as a'=(n-1)t/2R1R2.
Thus the system aberration coefficient of astigmatism takes
the form:
with the system P-V wavefront error W=aα2D2/4
(note that
σ2
is the stop separation for the secondary in units of its radius of
curvature).
For n~1.5, the meniscus' coefficient can be approximated by aL~t/4R1R2,
and taking R1~R2
gives aL~t/4R12.
With R12~-|tRP3|1/2/3,
the coefficient can be roughly approximated by
aL~-3|t/RP|1/2/4RP
which, for the typical average t/RP~0.02,
gives the meniscus' astigmatism as 1/10 that of the primary's
with the stop at its surface. Since mirror astigmatism changes with (1-σ1)2,
for the typical corrector-to-mirror separation σ1~0.4RP,
it gives corrector's astigmatism as aL/aP~-2|t/RP|1/2,
in units of the primary mirror contribution.
Again, as for the coma, this value needs to be adjusted for the weaker
corrector due to the presence of the secondary mirror. The adjusted value is
approximated by aL/aP~-2[|t/RP|(1-1.2k)]1/2.
This puts corrector's astigmatism
contribution to a system with the above parameters at nearly -1/4 that of the primary's.
For the average values of k~0.25, m~4 and σ1~0.4
(giving σ2'~-7.1),
the secondary's astigmatic contribution is nearly -0.5/RP,
or nearly 40% greater than that of the primary (~0.36/RP),
and of the opposite sign.
For smaller k and higher magnification m values, characteristic
of Gregory-Maksutov in general, the relative secondary contribution can
be considerably higher, mostly due to the increase in
σ2' (Eq. 132/131). Roughly,
astigmatic contribution in the typical Maksutov-Gregory is double that in
usually somewhat faster MCT with a larger, separated secondary. Thus, the secondary
contribution can be roughly approximated by
aS/aP~-1/12k2,
in units of the primary mirror astigmatic contribution.
Hence, the MCT system coefficient of astigmatism, as
a sum of its elements' contributions, is approximated by a~{1-2[|t/RP|(1-1.2k)]1/2-(1/12k2)}(1-σ1)2/RP.
 In the actual, typical MCT
configurations, similarly to coma, astigmatism is lower at f/10 than at
f/15, mainly due to the smaller secondary inducing roughly twice more
astigmatism. Both, meniscus and secondary induce astigmatism opposite to
that of the mirror, the former roughly 1/4 to 1/3 as much as the primary
(more at f/15 than at f/10), and the latter from about as much at f/10
to nearly twice as much at f/15 (both vs. primary's astigmatism with the
stop at its surface). Hence the astigmatism aberration
coefficient ranges from about 1/5 to about 6/5 of the mirror's (opposite
in sign). With the mirror aberration coefficient being aM=1/R
with the stop at its surface, reduced by a factor of (1-σ1)2
in an MCT,
and with the P-V wavefront error given by W=aα2D2/4,
taking 150mm aperture (so R=-900mm), σ1=0.4 and f/3 primary gives the
corresponding range of 1/16 to 1/2.7 wave P-V of astigmatism (0.013 to 0.074
waves RMS, for 550nm wavelength) at 0.5° off-axis, respectively.
Higher-order astigmatism is negligible.
Thus, MCT lower-order astigmatism
ranges from practically non-existent at f/10 to low, visually
inconsequential at f/15. However, the level of astigmatism directly
influences the best image field curvature. Typically, the combined
astigmatism of the meniscus and secondary, which is of the same sign, is
greater than astigmatism of the opposite sign induced by the primary.
Thus the system astigmatism is opposite in sign to the system Petzval,
hence making the best image surface less curved. However, with the
astigmatism being relatively low in comparison to the Petzval, best
image curvature remains generally strong (this concerns primary, or
lower-order astigmatism; higher-order astigmatism is
negligible).
Graph at left shows the
approximate magnitude of coma (combined lower and higher order) and
astigmatism for 150mm MCT, in the range from f/10 to f/15.
Image field
curvature in the MCT is, similarly to other two-mirror
arrangements, given in terms of the system's Petzval curvature R0
and aberration coefficient of astigmatism, as best, or median field
curvature:
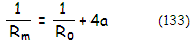
Note that the meniscus doesn't affect appreciably system's
Petzval curvature, which is
for all practical purposes determined by mirror radii.
EXAMPLE: Actual vs. approximated
level of coma and astigmatism in the 6" f/3/17
Gregory-Maksutov and 6" f/3/10 Maksutov-Cassegrain two-mirror system with a
separate secondary from
FIG. 119 (down-scaled to 6"). With t/RP
being 0.021 for both, and k=0.18 and 0.27,
respectively, the coma coefficient ratio approximation cL/cP~1.2|t/Rp|1/4(1-1.2k)1/2
gives the corrector lower-order coma
contribution of
about -0.4 and -0.37 in units of the primary's coma.
Adding the secondary contribution of nearly -3/4 and about -0.6 of
the primary's coma, respectively, according to
cS/cP~-0.32/√k,
gives the approximated system
lower-order coma sum of about -0.15 and 0.03 in units of the
primary's coma for the Gregory-Maksutov and system with separate secondary,
respectively.
The actual sums for the two
systems are -0.19 and 0.03 of lower-order coma, respectively, with the higher
order coma being nominally nearly 40% of the lower-order coma (thus
adding up) in the former, and nearly identical, but of opposite sign
(thus practically cancelling out) in the later. Approximations for
lower-order coma are close enough to be useful.
Approximate values for the
relative (in units of the primary's)
astigmatism aberration contribution for the Maksutov-Gregory and the
separate secondary MCT are, from
aL/aP~-2[|t/RP|(1-1.2k)]1/2,
-0.26 and -0.24 for the
two correctors and, from
aS/aP~-1/12k2, -2.5 and -1 for the secondary, respectively, in units
of the primary's astigmatic contribution. The actual system
contributions are -0.27/-0.22 and -2.3/-0.85, respectively. This
puts the system astigmatism sum approximation at about -1.8 and -0.24,
versus the actual -1.6 and -0.18, respectively. Again, not really
accurate, but sufficiently so to reflect gross proportions of the
individual elements' contribution and system error level.
Higher-order astigmatism in these
systems is generally negligible.
From the above approximation for
the system coefficient of astigmatism, it is a~0.0007 for the
Maksutov-Gregory (slightly more than given with Eq. 132).
With the system Petzval surface obtained from
Eq. 30, best image surface
curvature is, from Eq. 133, approximated as Rm~-190mm. The
actual value for the system is -210mm, which is close enough for the
initial assessment. For the system with separated secondary, the
value of aL
is only slightly (~10%) smaller, but the approximated astigmatism is
nearly 1/4 of that of the primary, so that the system astigmatism
coefficient (approximation) comes to a~0.00015. With that value, best (median) image curvature approximation
for this system is Rm~-345mm,
with the actual best field curvature Rm~-360mm.
The discrepancy is mainly
caused by somewhat greater actual values for k, m and
ρ than those obtained from two-mirror relations, the result
of the power of meniscus corrector. For a quicker, and fairly
accurate estimate of the median image curvature in an MCT, in a
typical system it can be expected to be numerically quite
close to the secondary mirror radius of curvature.
Misalignment aberrations
Off axis aberrations described above are those of perfectly aligned
systems. Actual units are commonly misaligned to some degree, and
that changes their field aberration map. Below is a raytrace of
two main variaties of Maksutov-Cassegrain telescope these days,
(A) with aluminized spot on the meniscus and aspherized primary, and
(B) with separated secondary, all spherical. The former can use
significantly faster primary for a similar level of the central line
correction.
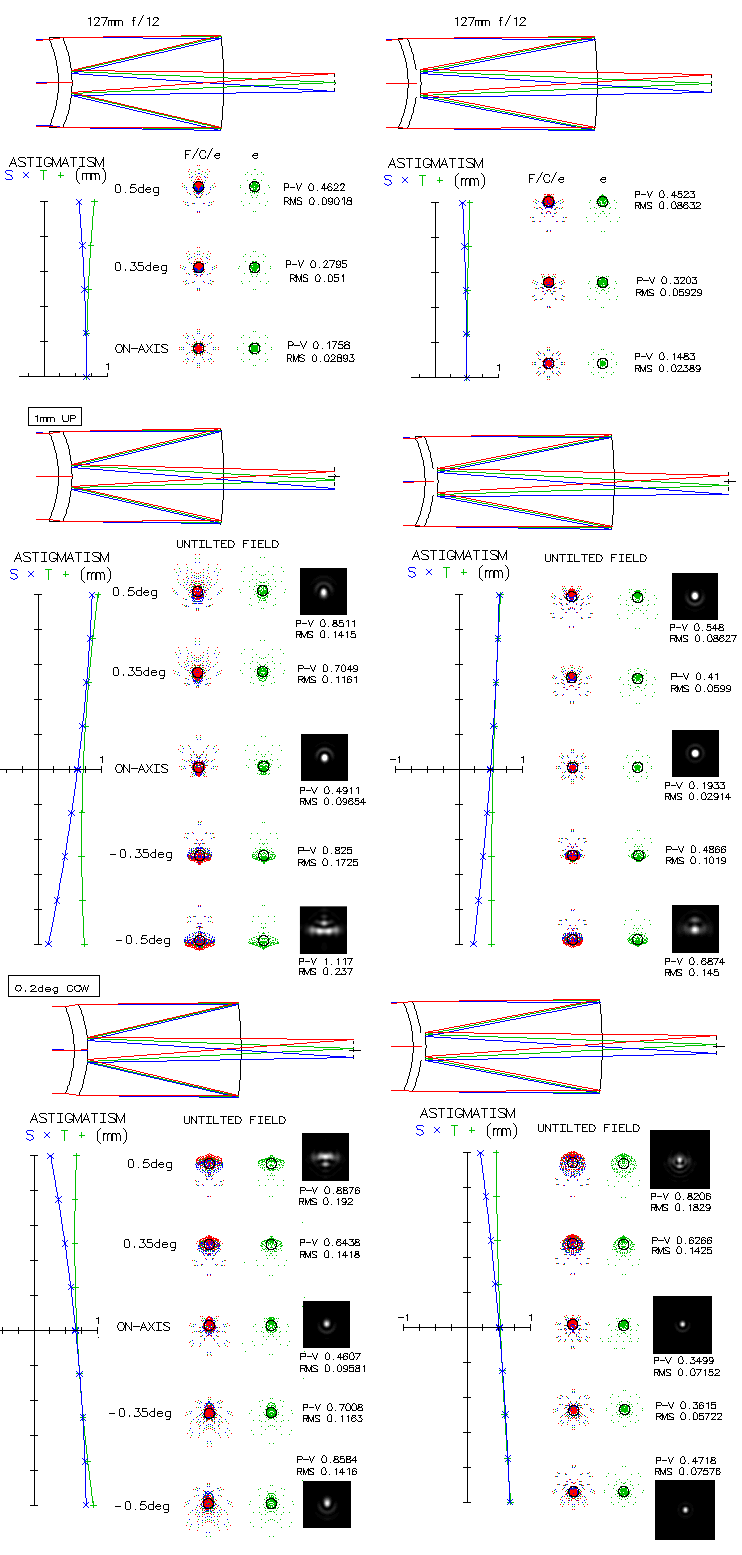
Perfectly aligned, the systems have radially symmetrical field with
similar level of aberrations (top). Decentering meniscus 1mm up
changes the astigmatic field and induces negative all-field coma.
Astigmatic field becomes asymmetric in the directional plane of
decenter, with astigmatism intensifying over field radius opposite
to the decenter direction, and diminishing over the other half.
Astigmatism dominates on one side, and coma dominates on the other,
with the spot meniscus inducing significantly more coma than in the
system B. Optical axis is shifted about 0.25° below physical
field center, but it is relatively insignificant since the best focus,
roughly about a third of that distance toward optical center, is
only marginally better. In the field center coma dominates in the
system A, creating error significantly stronger than in the system B,
where coma and astigmatism in the field center are negligible.
Tilting meniscus 0.2° counterclockwise (top away from the primary)
induces similar change to the astigmatic field, but of opposite
sign (secondary in the system B is assumed to be aligned with the
meniscus). This time, optical field center is shifted above
physical field center (approx. 0.15°), and best focus in
its proixmity. System B is again significantly less affected than
system A. The difference between the two mainly comes from system A
being practically coma-free when perfectly aligned, while system
B has some residual negative coma (about 0.4 wave P-V at 0.5°).
Unlike system A, where secondary and rear meniscus surface
cannot be mutually misaligned, system B has additional level of
complexity since its secondary can be misaligned vs. meniscus.
Secondary tilt alone induces negative all-field coma counterclockwise, and
positive when tilted clockwise. In this case, 0.2° secondary
tilt induces over 0.5 wave P-V, which means that one side of the
field in the plane of tilt gets coma added to the existing coma
and the opposite side gets it deducted. Meniscus decenter up partly
offsets its CCW tilt with respect to the astigmatic field deformation
and coma (with the secondary aligned with rear meniscus surface).
Tilt of primary alone also induces field center aberrations, as well
as astigmatic field asymmetry (below, system B).
Tilt causes optical axis to sink nearly 1/2 degree, hence astigmatic
field around optical center (left) is not representative, with astigmatic
field across the actual field being constructed next to it (right).
Astigmatism dominates lower half, and coma the upper half of the
field diameter in the plane of tilt. Image tilt is 1.3° and
could affect its appearance even if eye can accommodate, since
only one side at the time can be in focus. In general, magnitude of
aberrations induced is in proportion to the nominal misalignment.
Note that the primary decenter alone has the same effect as that of
meniscus with secondary.
◄
10.2.3.4. MCT aberrations: spherical
▐
10.2.4. Full-aperture Houghton corrector
►
Home
| Comments |