◄ 3.5.3. Zernike expansion schemes   ▐    4.1.2. Lower-order spherical: aberration function ►

As mentioned, these are the aberrations caused by the inherent properties of properly positioned optical elements, thus caused either by the aberration limitations of a conic surface, or fabrication error (i.e. error in surface radius or conic). They are identical in form to the corresponding aberration caused by miscollimation, but they cannot be eliminated in the alignment procedure.

Intrinsic telescope aberrations include the five primary aberrations intrinsic to conical surfaces of revolution - spherical, coma, astigmatism, field curvature and distortion - as well as chromatism and wavefront aberrations resulting from fabrication errors.

Limiting to the monochromatic aberrations of a conic surface, they originate from optical path difference between chief ray and all other rays. In its basic form, it is expressed as a polynomial containing all determining factors: object-to-image point separation, angles of incidence and refraction/reflection, pupil coordinates, surface radius of curvature and surface conic. Since this polynomial is under square root, it is converted, through binomial expansion, into a series of terms, starting with those largest in magnitude, toward an arbitrary number of progressively smaller ones. In general, the largest terms are called primary aberrations, the next largest group being secondary aberrations, and so on. Optical path difference for all rays defines surface of the wavefront, and it in turn determines wave/phase combining in the image space.

Plots below show the aberration terms, with primary aberrations being generally the largest in magnitude, followed by secondary and tertiary aberrations. Each term contains aberration coefficient, _ja_nm, where the subscripts, in a simplified interpretation, are exponents over point height in image space h (subscript j), in-pupil height ρ (subscript n), and pupil angle θ (subscript m). The coefficient determines the magnitude of aberration, parameter h shows how it changes with the height in the image space, and parameters in ρ and θ determine shape of the wavefront in the pupil. All terms are defined for paraxial focus on axis, and the Gaussian image point for abaxial points, but the minimized - i.e. balanced with one or more other aberrations - forms are also shown (height of the balanced forms is proportional to the P-V error reduction).

Among primary aberrations, tilt does not affect the wavefront shape, only its orientation; it merely shifts point image to a different location. Similarly, defocus is not inherently an aberration, since it only exists when point of observation is longitudinally displaced from the focus point. Remaining three primary aberrations do change wavefront shape away from spherical, i.e. they change the quality of point-image itself. Primary spherical aberration is independent of field angle, and can be minimized by balancing it with defocus of opposite sign. Primary coma has an inherent tilt error component, which means the wavefront axis is not directed toward Gaussian focus point (the 3-fold reduction in the P-V wavefront error by correcting for the tilt is fictitious, because it doesn't change the point-image itself; it merely signifies switching from a reference sphere centared at the Gaussian focus to one centered at the point shifted laterally from it, for which the wavefront tilt is eliminated - there is no such thing as "lateral defocusing"). Primary astigmatism gives to the wavefront deviation cylindrical shape which, since changing with the square of in-pupil height, has parabolic profile; such wavefront forms a line-like point image. Adding defocus of opposite sign changes the form of wavefront deviation, producing more desirable, round ray spot plot, and an image with a four-fold symmetry. Similarly to spherical aberration, where the best (defocused, i.e. balanced with defocus) image is found by re-focusing to the point midway between paraxial and marginal focus, best astigmatic image is found by refocusing to the point midway between tangential and sagittal focus. With the common, field astigmatism, usually associated with field curvature, best astigmatic focus is subject to eye accommodation.

Aberration forms remain fairly similar from the 4th (primary) to the 8th order (tertiary). Somewhat different is secondary aberration known as trefoil. This aberration term has an overall similarity to coma, except that it has no lobes (hence its name elliptical coma; also known as arrows, somewhat loosely from German pfeilfehler). It is very rare in practice in its basic form, possibly because it may tend to be associated with coma. In its original form, similarly to astigmatism, focuses into a line, but due to the two opposite sides of the wavefront having the same orientation, this line forms on one side of the Gaussian focus. 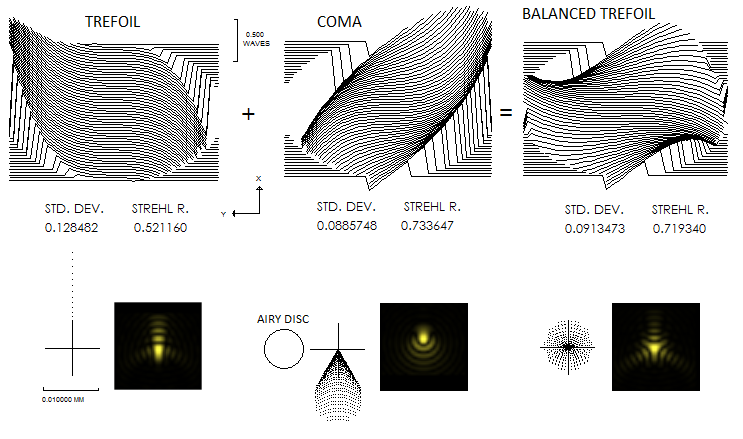When combined with primary coma of opposite sign, it produces what most people associate with the name "trefoil" (below).

The original trefoil form (left) already produces diffraction image with a three spike symmetry, but the vertical spike is noticeably more pronounced than the two angled ones. Balancing coma is of the same P-V wavefront error, of opposite sign. The resulting Strehl is lower than for unbalanced trefoil, but the ray spot plot is rotationally symmetrical, and the diffraction image also becomes 2-D spatially symmetrical (3-fold symmetry). Note that wavefront plots for all three are shown uncorrected for tilt (the only mode with this ancient version of SYNOPSYS), but the RMS/Strehl values are for the best focus location (note that diffraction images are not in proportion to the ray spot plots and associated Airy disc).

Not shown among secondary aberrations are lateral spherical aberration, ₂a₄₀, which has the same form as primary spherical, but depends on the square of field angle, lateral coma, ₃a₃₁, of the same form as primary coma but dependant on the cube of field angle, lateral astigmatism, ₄a₂₂, of the same form as primary astigmatism, but increasing with the 4th power of field angle, as well as lateral distortion, ₅a₁₁, increasing with the 5th power of field angle, and lateral field curvature, ₄a₂₀, increasing with the 4th power of field angle. Oblique, or lateral spherical is somewhat ambiguous, since SYNOPSYS gives it as tangential and sagittal, implying it is changing with pupil angle. Also, what Mahajan gives as "secondary astigmatism" (called "wings", or Flügelfehler - dragonfly), which is also the basis for Zernike secondary astigmatism, Sasian gives as "un-named", while as secondary astigmatism gives what is with Mahajan "lateral astigmatism" (plots above are according to Mahajan). Appears as if there is no consensus about higher-order aberrations' terminology. There is roughly twice more tertiary, than secondary aberrations, but only a few are shown to illustrate how the form changes from lower toward higher order aberrations. Quatrefoil can be also balanced with either primary, or tertiary astigmatism, but the reduction is less pronounced than with secondary astigmatism and defocus.

Specific notation for the five conic surface aberrations is based on a power series expansion of the aberration function that sums up all the geometric deviations in point imaging for Gaussian image point, in which a general aberration term is given as 2l+mwnmdnh(2l+m)cosmθ, where w, d, h and θ are the aberration coefficient, pupil radius, point height in the image space and pupil angle, respectively, and l, m, and n are the power terms from the function. The latter are associated with specific aberrations as shown in table below.

Wavefront aberration forms with 2l+m+n=4 are called 4th order or primary aberrations, those with 2l+m+n=6 are 6th order, or secondary, those with 2l+m+n=8 are 8th order or tertiary, and so on.

The entire term constitutes the peak aberration coefficient, equaling the value of the peak (coma, tilt), or peak-to-valley (spherical, astigmatism, field curvature) wavefront error at the Gaussian image point.  For primary spherical, it is paraxial focus, where the P-V wavefront error changes with (ρd)4, ρ being the height in the pupil normalized to 1. Thus, for unit radius, it is proportional to ρ⁴, which is its aberration function. For coma, the P-V wavefront error changes with (ρd)³, i.e. in proportion to ρ³, and so on (with 0≦ρ≧1). Strictly talking, these are Siedel aberrations, but best (diffraction) focus is shifted away from the Gaussian image point, as given in Table 3.

Sum in the last column is the order of the aberration term. Fourth order wavefront aberrations are called primary, and sixth order aberrations are called secondary aberrations (since this sum is smaller by one for transverse ray aberrations, primary aberrations are also called third order, and secondary aberrations fifth order).

For practical purposes, the front subscript is often omitted, with the aberration coefficient identified only as w nm. The subscript is sometimes entirely omitted, for simplicity, as it is in this text, where aberration coefficients for primary spherical aberration, coma, astigmatism and field curvature are denoted by s, c, a, p and g, respectively, with the corresponding peak aberration coefficients S, C, A, P and G. Aberration coefficients for secondary aberrations are more complex and are not specified, but secondary aberrations are described and illustrated for the three point-image quality aberrations, spherical, coma and astigmatism.

This nominal notation can also be used to identify the aberration with Zernike coefficients.

4.1. Spherical aberration

Spherical aberration - or correction error - is the only form of monochromatic axial aberration produced by rotationally symmetrical surfaces centered and orthogonal in regard to the optical axis. The attribute spherical probably originates in this aberration being inherent to the basic optical surface - spherical - for object at infinity. However, spherical aberration will appear whenever optical surface form doesn't properly match that of the incident wavefront. Thus, it is induced with the change of object distance or, with multi-surface objectives, with deviations in proper spacing. Spherical aberration affects the entire image field, including the very center. For that reason, its correction in a telescope is more important than that of other inherent conic surface aberrations, which affect the outer field.

Spherical aberration in the majority of amateur telescopes - especially more traditional ones, like Newtonian reflector or achromat refractor - is sufficiently accurately presented based on the 4th order surface approximation, which includes the first two terms in the conic surface expansion series. Axial aberration associated with this surface approximation is called lower-order, or primary spherical aberration (also, 4th order wavefront, or 3rd order transverse ray aberration). Telescope objectives with strongly curved surfaces - like Maksutov-Cassegrain or doublet apochromatic refractors - generate significant amount of higher-order (6th on the wavefront, or 5th transverse ray) spherical aberration, which requires inclusion of the third term in the series i.e. upgrading, or correcting 4th order surface approximation to the 6th order surface. Very rarely, yet higher order terms also need to be taken into account.
 

4.1.1. Lower-order (primary) spherical aberration

FIG. 33 illustrates under-corrected (negative) form of primary spherical aberration, characteristic of a spherical mirror for object at infinity. Due to the actual wavefront being not spherical, rays projected from it do not meet at the same point; the wavefront becoming more strongly curved toward the edge causes the foci for rays projected from its outer zones to fall progressively closer to the mirror.

With over-corrected (positive) spherical aberration, marginal rays focus farther away than paraxial rays. In either case, geometrical structure of the defocused zone remains identical in regard to the paraxial focus.