|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.2.3. Two-mirror telescopes
▐
8.3.1. Paul-Baker, flat-field
anastigmatic aplanats
► 8.3. Three-mirror telescopesPAGE HIGHLIGHTS While amateur telescopes and cameras with more than two power mirrors are relatively rare, there are three-mirror designs that deserve mention, being relatively easy to make and offering exceptional performance. Addition of the third mirror imposes additional demands in regard to fabrication and makes alignment more difficult. On the other hand, it allows for better correction of aberrations, sometimes with easier to make surfaces. The presence of a third mirror also makes the aberration relations more complex. In effect, aberrations of the third mirror are added to those of the primary and secondary. This means that the starting point are the two-mirror system aberration relations. For the first two mirrors in a three-mirror system, they are identical to Eq. 78-78.1 given for two-mirror systems. Aberration relation for the tertiary is identical to that for the secondary in its general form, but there are differences in the parameter values, such as the actual angle of incidence for off-axis points, effective stop displacement, sign, and others. For the primary mirror, the P-V wavefront error at the best focus for spherical aberration, coma and astigmatism is given by:
respectively, with K1 being the primary conic, D1 the aperture diameter, F the focal ratio, α the field angle, and h the height in the focal plane. For the secondary,
and for the tertiary
in the same order, with K2/3 being the secondary/tertiary conic, D2/3 the secondary/tertiary minimum aperture (the cone width at the mirror), R2/3 the secondary/tertiary radius of curvature, Ω2/3 the relative inverse of the object distance ℓ2/3 in units of the radius of curvature (Ω2=R2/ℓ2, and Ω3=R3/ℓ3, with object, as before, being the image formed by preceding surface) for the secondary/tertiary, and σ2/3 the secondary/tertiary to the aperture stop separation in units of secondary/tertiary radius of curvature. The angle α'=[(R1/R2)+(1/m2)]α, at the tertiary is the magnified field angle α after reflection from the secondary. For the tertiary, the aperture stop location is the image of the primary mirror formed by the secondary, which is at the distance I2=s2+s2R2/(2s2+R2) from the primary, s2 being the primary-to-secondary separation. For the Cassegrain arrangement (secondary inside the primary focus), both s2 and R2 are numerically negative, and so is I2, which means that secondary's image of the primary forms to the left of primary, farther away from it than the secondary; since the tertiary is usually (in axial systems) between the primary and secondary, tertiary-to-stop separation is given by S3=s2-s3, with s3 being tertiary-to-primary separation (also numerically negative); from this, σ3=s3/R3. The combined system P-V wavefront error for each aberration is the sum of aberrations on each mirror, thus W=W1+W2+W3. Corresponding RMS wavefront errors are given in sections covering specific aberrations. With the system astigmatism corrected, best image surface coincides with the system's Petzval surface, which is given by rP=(2/R1)-(2R2)+(2/R3), with R1/2/3 being the radii of curvature for the primary, secondary and tertiary mirror, respectively. THREE MIRROR SYSTEMS EXAMPLES
It is well known that the Gregorian can be folded, in order to reduce its length,
by placing a flat at a location of the Cassegrain secondary, which then sends the
final beam through the Gregorian secondary located in front of the primary. Such system
can be made aplanatic by putting a mild curve on the front mirror, which then becomes the secondary, while
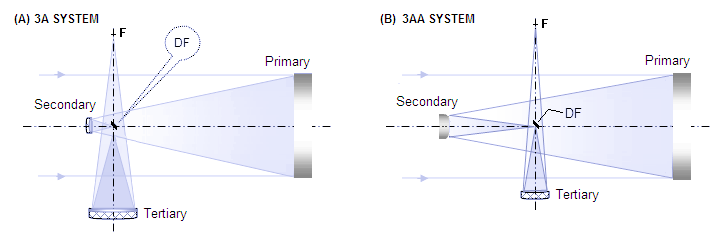
the Gregorian secondary becomes the tertiary (with the secondary being also the quarternary, being the place of last reflection). Follow two examples of three-mirror systems that I haven't seen elsewhere. One is an aplanat with spherical primary and secondary, and the other is anastigmatic aplanat with two moderately strong prolate ellipsoids (including primary) and a sphere (FIG.128). The two are folded three-mirror Cassegrain-Gregorian systems, 3A and 3AA (for "aplanat" and "anastigmatic aplanat", respectively, with some unique qualities. The former is aplanatic system consisting from three concave mirrors, spherical primary and secondary, with the tertiary being a weak but strongly curved ellipsoid (FIG. 128 A). Mirrors are easy to make, and the only disadvantage is comparatively more difficult collimation. The tertiary is significantly more sensitive to misalignment than secondary; in the f/4.25 3A system
described below it is about 2/3 as sensitive to angular tilt as the 300mm primary. It is the level of tilt sensitivity of a 300mm f/4 paraboloid. Also, the tertiary is more than twice as sensitive to decenter than secondary in an f/8 Ritchey-Chretien of equal aperture (despace is comparatively forgiving). This level of miscollimation sensitivity would demand very accurate and stable alignment mechanism. Various arrangements are possible, differing in mirror size, location, conic (for instance, larger secondary can be aspherised to correct coma, with less aspherised secondary correcting for spherical aberration, resulting in significantly lower astigmatism), or relative aperture of the system. Prescription for an actual f/4.25 system with an f/3 primary, that can be scaled to both aperture and primary focal length is as follows: σ1 = 0.4583, σ2 = -0.1889, ρ2 = -ρ3=-0.2111, K1,2 = 0, K3=-0.396 where σ1 and σ2 are, as before, primary-to-secondary and secondary-to-tertiary separation, respectively, and ρ2 and ρ3 are secondary and tertiary radius of curvature, respectively, all expressed in units of the primary radius of curvature. This determines relative marginal ray height on the secondary k2=0.083, in units of the aperture radius, and secondary magnification m2=ρ2/(ρ2-k2)=0.72. With the actual cone angle being expanded by a factor of 1/m2 toward tertiary, marginal ray height at the tertiary k3=(2σ2/m2)-k2=-0.44. With ρ3 also effectively greater by a factor of 1/m2, ρ3e=ρ3/m2=-0.293, and the tertiary magnification m3=ρ3e/(ρ3e-k3)=-2. Best (median) field curvature is ~0.2f, f being the system focal length. Effective central obstruction υ in units of the aperture (linearly), is given by: υ = 2F1m2m3α/(m3-1)k3, with F1 being the primary focal ratio, α the field angle in radians (m3 and k3 as absolute values). Alternatively, the angular field radius in terms of the relative obstruction radius o in units of the aperture radius is given by α=o(m3-1)k3/2F1m2m3. For F1~3, m2~0.72, |m3|~2, and |k3|~0.44, an effective 0.2D obstruction would produce ~° field radius. Diffraction limited field is set by astigmatism. For the above f/4.25 system, it is at the level of a f/5.6 paraboloid. Despite its magnitude in the outer field of the objective's image, astigmatism is not likely to be objectionable in visual use, due to the offset with even stronger astigmatism of conventional eyepieces. However, due to large relative apertures, good field definition here would require eyepieces well corrected for higher-order astigmatism. The other folded Cassegrain-Gregorian system, anastigmatic aplanat 3AA (FIG. 81B), can be made in various arrangements. One example with the minimum secondary size of 0.25D and that of the tertiary of 0.2D has the following parameters: σ1 = 0.375, σ2 = -0.3, ρ2 = 1, ρ3 = 0.19375, K1 = -0.727, K2 = 0, and K3 = -0.576 with best field curvature rc~0.1R1. An f/3/10.6 D=400mm 3AA system still has as high as 0.998 Strehl near the limits of the standard visual field, at 0.3° (22mm) off-axis. Since the field curvatures of the primary and secondary exactly offset each other, the system curvature is given by rC=R3/2. For the lower system curvature with given primary, the secondary needs to be more curved, and the tertiary less. Sensitivity to decenter and tilt of the tertiary in the 3AA is several times lower than in the 3A system. Forfeiting visually accessible final focus allows to design three-mirror systems that in addition to being anastigmatic aplanats also have - or can have - flat field. Those include Paul-Baker curved and flat-field variants, as well as two other less known three-mirror flat-field anastigmatic aplanats that I came up with not long ago. I haven't searched them for originality, so let's term them as FAA1 and FAA2.
|
